The volume of the solid obtained by rotating the region bounded by the curves `y=2 x/2, y=0, x=1,x=2` , about x axis, can be evaluated using the washer method, such thatY = 1/x, y = 0, x = 1, x = 3;Example Find the volume of the solid obtained by revolving the region bounded by y= x2, y= 0, x= 1, and x= 2 about the line x= 3 Using the Shell Method, V = 2ˇ Z 2 1 (3 x)x2dx = 2ˇ Z 2 1 (3x2 x3)dx = 2ˇ x3 1 4 x4 2 1 = 13ˇ 2 Example Find the volume of the solid obtained by revolving the region bounded by y= p x and y= x2 about the line
Volume Of Revolution Of Solid Formed By Y X 2 And Y 2x About Y Axis Mathematics Stack Exchange
Y=x^3 y=0 x=1 about x=2 washer
Y=x^3 y=0 x=1 about x=2 washer-Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreFeb 07, 17 · 72 Finding Volume using the Washer Method Example 1) Find the volume of the solid formed by revolving the region bounded by the graphs y = √x and y = x 2 about the xaxis


4a Volume Of Solid Of Revolution By Integration Disk Method
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreHow to solve Determine the volume of the solid of revolution generated by revolvling the region bounded by y = x^3 x^5, y = 0, x = 0, and x = 1Oct 01, 19 · 1 in x 1/2 in Rigid Conduit Reducing Washer (2Pack) Use a pair of 1 in x 1/2 in Rigid or IMC Use a pair of 1 in x 1/2 in Rigid or IMC Conduit Reducing Washers (2Pack) to reduce the knockout in a steel outlet box or similar enclosure Each washer has a raised flange for positive seating Corrosion resistant
Apr 16, 15 · How do you find the volume of the solid generated by revolving #y=10/x^2#, #y=0#, #x=1#, #x=5# about the yaxis?Calculus Applications of Definite Integrals Determining the Volume of a Solid of Revolution 1 Answer How do you find the volume of a solid of revolution washerUse the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the axis Sketch the region and a
Square washers fit into slots and channels and have flat sides to keep them from rotating They are wider and thicker than most round washers, making them good for distributing heavy loads Blackoxide steel washers are mildly corrosion resistant in dry environments Zincplated steel washers are corrosion resistant in wet environments Galvanized steel washers are 10 times as corrosionGive reasons for your answersANSWER IS Solution For a differential equation M(x,y) dx N(x,y) dy= 0 The necessary and sufficient condition for exact differential equation is ∂M/∂y = ∂N/∂x Here the equation is not exact if M(x,y) dx N(x,y) dy = 0 is of the from f(x,y)y dx g


Volume Of A Solid Of Revolution Disks And Washers



Volume Of Revolution Of Solid Formed By Y X 2 And Y 2x About Y Axis Mathematics Stack Exchange
Sketch the region, the solid, and a typical disk or washer {eq}\displaystyle y = x^3,\ y = 0,\ x = 1 {/eq};Jan 13, 17 · S=7/6 First we note that 1/x^2 > 0 for any x so the intercept between the curves and the xaxis must belong to the curve y=x and in fact occurs for x=0 Then we analyze the inequality xSketch the region, the solid, and a typical disk or washer y = x 3 , y = 0, x = 1;
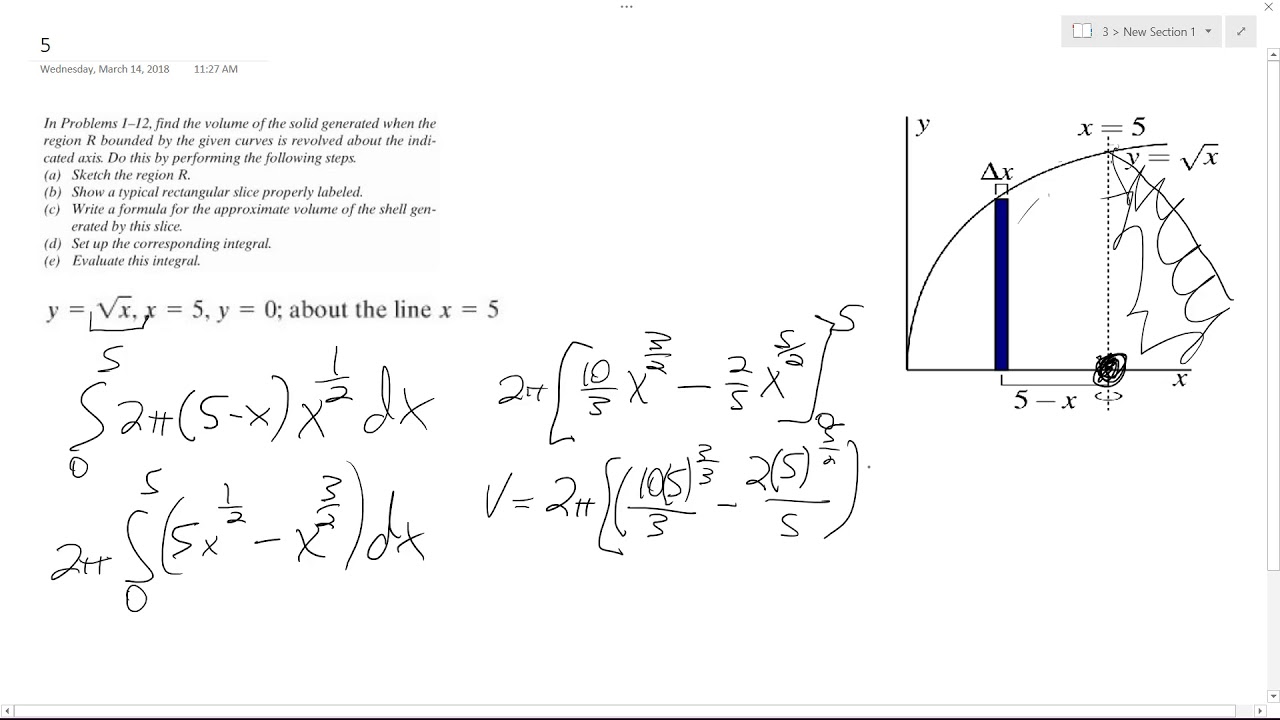


Y Sqrt X X 5 Y 0 About The Line X 5 Youtube
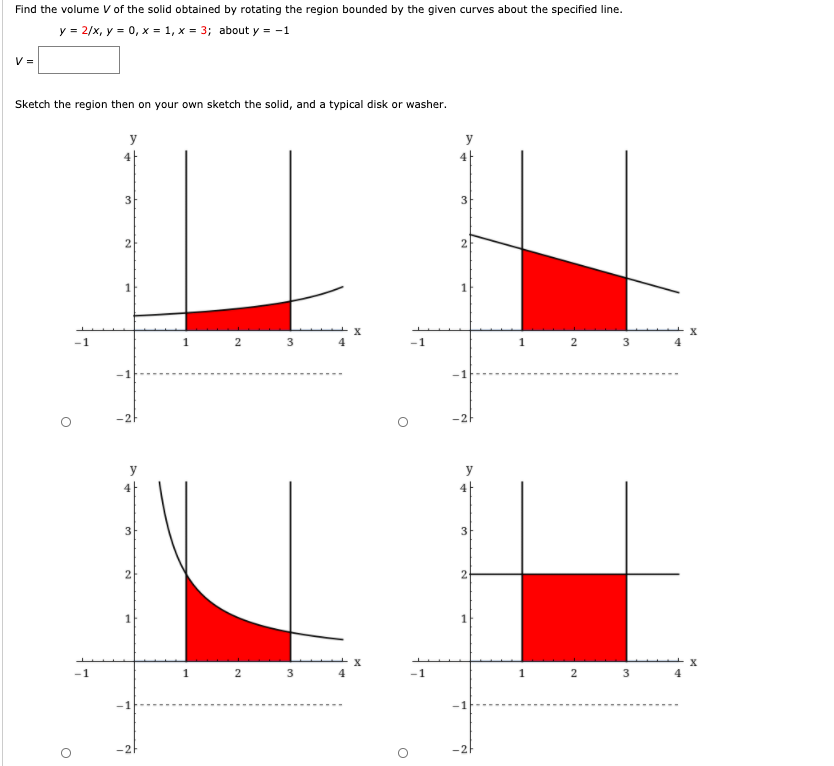


Solved Ind The Volume V Of The Solid Obtained By Rotating Chegg Com
Answer to Find the volume V of the solid obtained by rotating the region bounded by the given curves about the specified line y = 27x^3, y = 0, xFind the volume of the solid obtained by rotating the region bounded by the given curves about the specified line {eq}1 y = x^3,y= 0, x=1 \text{ about } x= 2 \\ 2In mathematics, the degree of a polynomial is the highest of the degrees of the polynomial's monomials (individual terms) with nonzero coefficients The degree of a term is the sum of the exponents of the variables that appear in it, and thus is a nonnegative integerFor a univariate polynomial, the degree of the polynomial is simply the highest exponent occurring in the
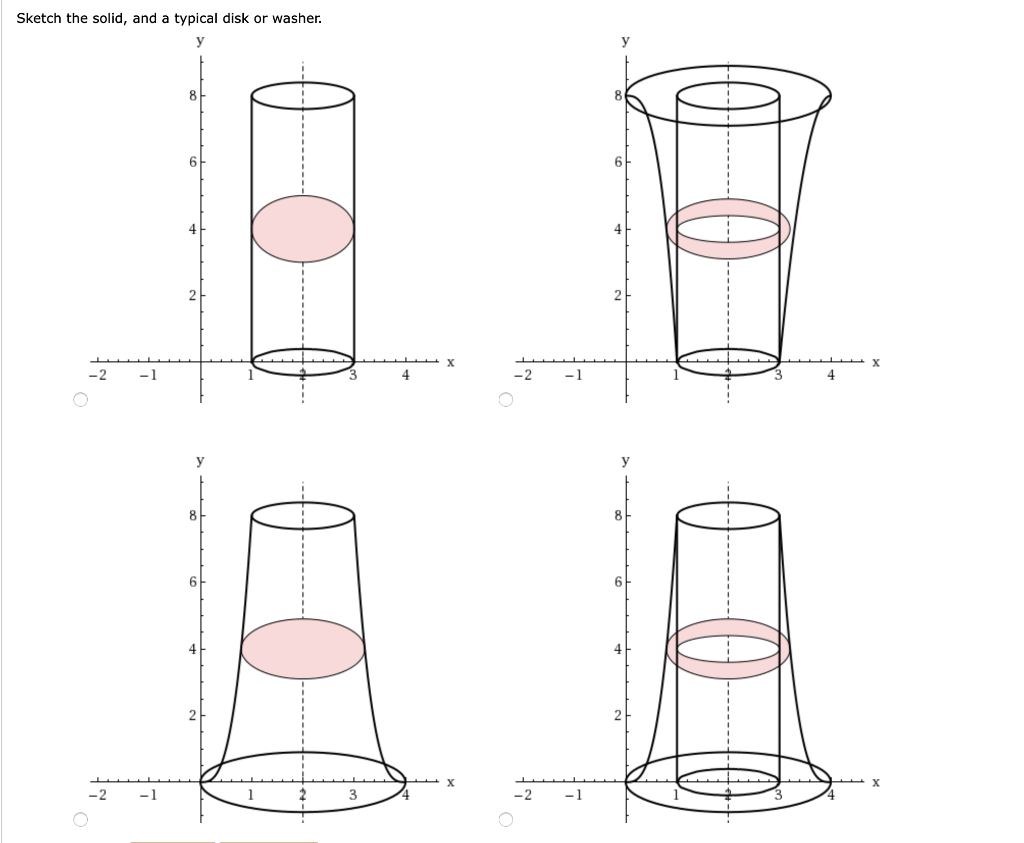


Solved Find The Volume V Of The Solid Obtained By Rotatin Chegg Com
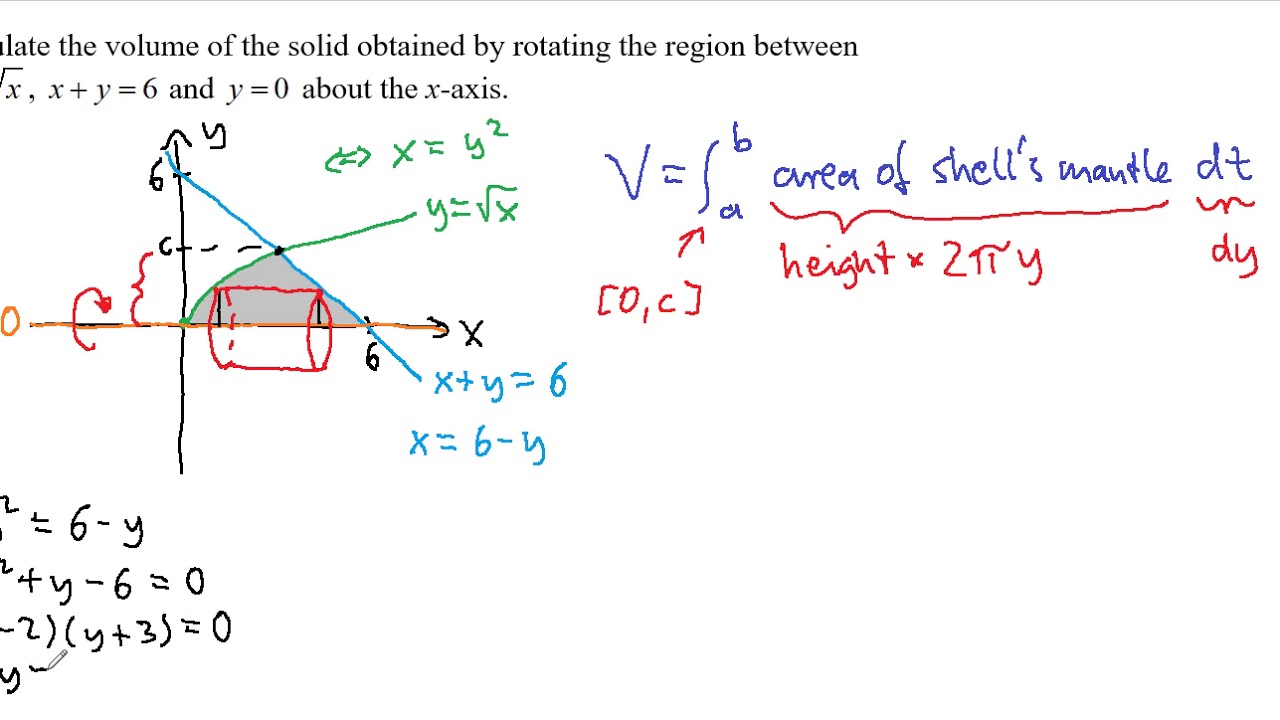


Volume Of Revolution Shell Method
Steps for Solving Linear Equation ( x ^ { 3 } y ^ { 2 } ) d x 3 x y ^ { 2 } d y = 0 ( x 3 y 2) d x − 3 x y 2 d y = 0 To multiply powers of the same base, add their exponents Add 2 and 1 to get 3 To multiply powers of the same base, add their exponents Add 2 and 1 to get 3About {eq}\displaystyle x = 2 {/eq} Finding the Volume of the Solid of RevolutionThe cross sections of Sare washers with area A(x) = ˇ(outer radius)2 ˇ(inner radius)2 = ˇ(f(x) c)2 ˇ(g(x) c)2 Hence the volume of such a solid is given by V = Z b a ˇ(f(x) 2c)2 ˇ(g(x) c) dx Example What is the volume of the solid generated by rotating the region bounded by the curves y= x2 and y= p xand the lines x= 0 and x= 1 about the


Solved Find The Volume V Of The Solid Obtained By Rotatin Chegg Com
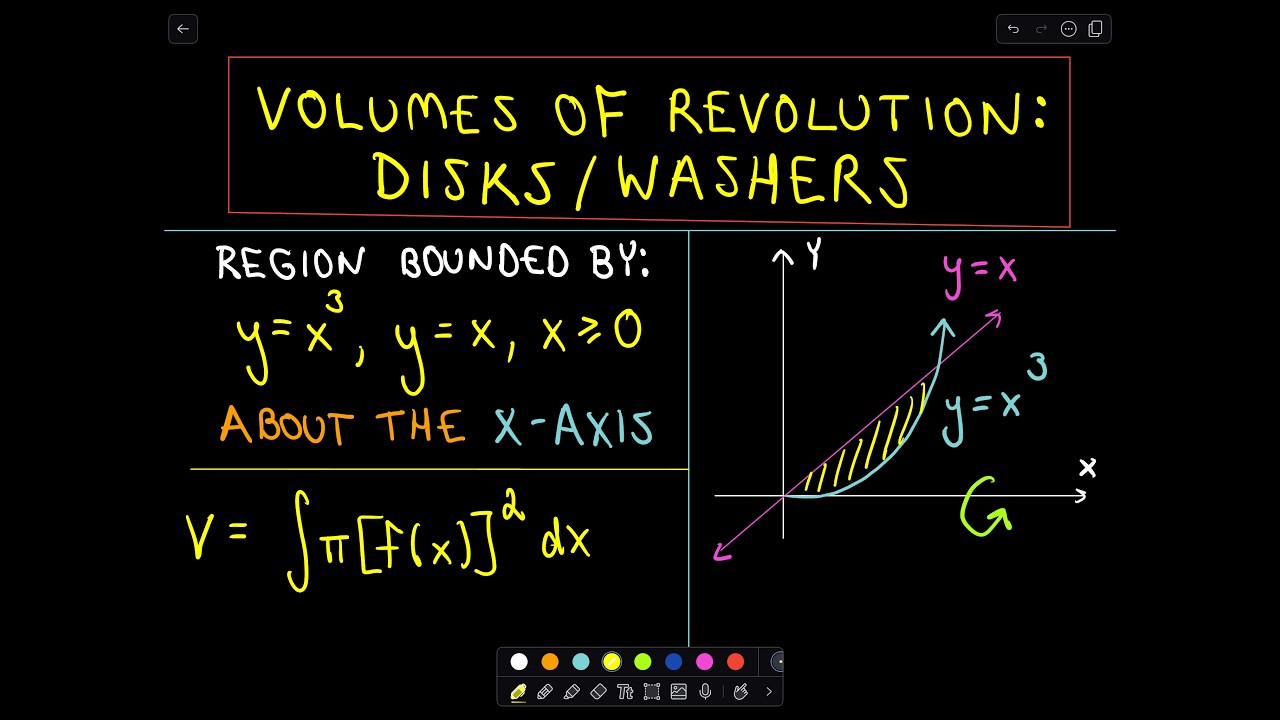


Volumes Of Revolution Disk Washers Example 1 Youtube
Jun 09, 18 · Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries Students (upto class 102) preparing for All Government Exams, CBSE Board Exam, ICSE Board Exam, State Board Exam, JEE (MainsAdvance) and NEET can ask questions from any subject and get quick answers byHow many integrals would be required in each case?The washer method is used to evaluate the volume of the solid formed by rotating the region between curves about a given axis of rotation If the region



Volume Of Revolution Shell Method


Calculus I Volumes Of Solids Of Revolution Method Of Rings
Calculus Applications of Definite Integrals Determining the Volume of a Solid of RevolutionY=x3x212x No solutions found Rearrange Rearrange the equation by subtracting what is to the right of the equal sign from both sides of the equation y(x^3x^212*x)=0 How do you graph the function, label the vertex, axis of symmetry, and xinterceptsQuestion Y=x^3 Y=0 X=1 X=2 About Y Axis This problem has been solved!



Using The Disk Method Or Washer Method Find The Volume Of Y X 3 Y 1 X 2 Revolving Around The X Axis Study Com
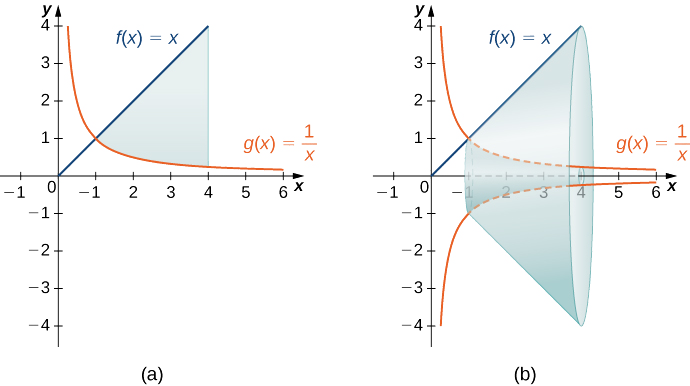


6 2 Determining Volumes By Slicing Mathematics Libretexts
See the answer y=x^3 y=0 x=1 about x=2 Best Answer 100% (4 ratings) Previous question Next question Get more help from Chegg Solve it with our calculus problem solver and calculatorYou need to evaluate the volume of the solid obtained by the rotation of the region bounded by the curves `y = x^3 , y = 0, x = 1` , about x = 2, using washer method, such thatCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history



Solved Part 2 12 Find The Volume Of The Solid Obtained Chegg Com



Solved 1 The Volume Of The Solid Obtained By Rotating Th Chegg Com
Find the Volume y=1/x , x=1 , x=2 , y=0 y = 1 x y = 1 x , x = 1 x = 1 , x = 2 x = 2 , y = 0 y = 0 To find the volume of the solid, first define the area of each slice then integrate across the range The area of each slice is the area of a circle with radius f (x) f ( x) and A = πr2 A = π r 2Apr 02, 17 · How do you find volume by rotating area enclosed by #y=x^3# and #y=sqrt(x)# about x=1?Jun 10, 18 · pi/ units ^3 We need to find where these two curves intersect to find the bounds of integration y^2=x^3 and y=x^2, squaring the second expression, y^2=x^4 Solving for y^2, x^4=x^3 ie, x^3x1=0 So x=1, x=0 are the points of intersection From the graphs of these expressions in can be seen that y=sqrtx^3 has a greater area than y= x^2 so we must find the area under y =x^2
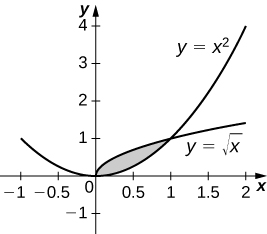


6 2 Determining Volumes By Slicing Calculus Volume 1
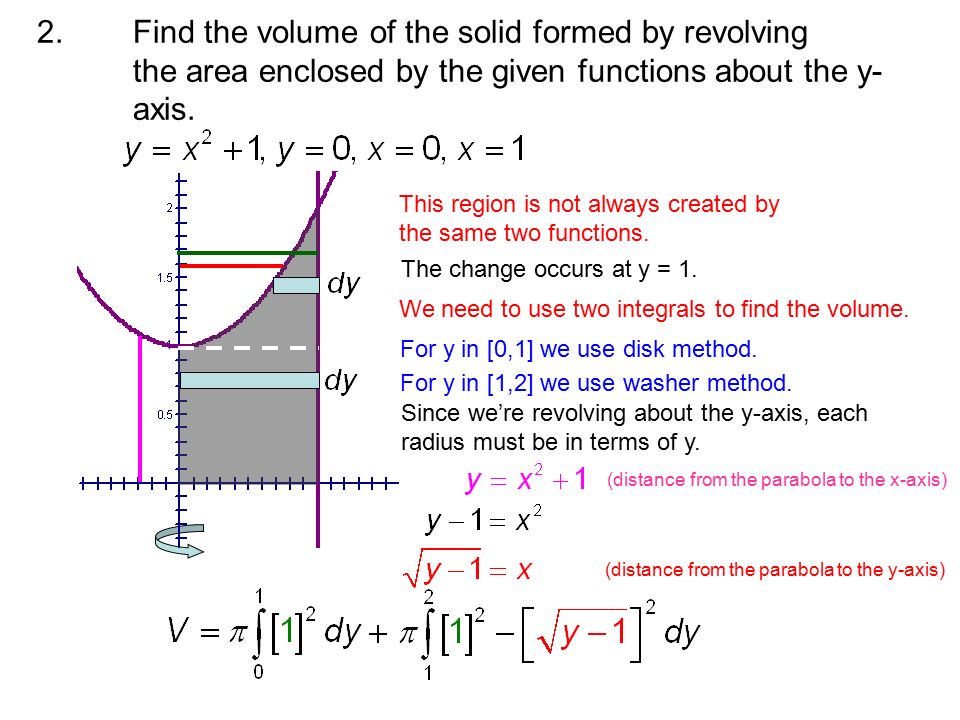


Volume The Disc Method Ppt Video Online Download
#10 x 1" OD Stainless Fender Washer, (100 Pack) Choose Size, by Bolt Dropper, 1 (304) Stainless Steel 48 out of 5 stars 1,973 $1285 $ 12 85 Save 5% on 2 select item(s) Get it as soon as Fri, May 14 FREE Shipping on orders over $25 shipped by Amazon 11/4" ID USS Flat WashersSee the answer y=x^3 y=0 x=1 x=2 about y axis Expert Answer 100% (2 ratings) Previous question Next question Get more help from Chegg Solve it with our calculus problem solver and calculatorQuestion Y=x^3 Y=0 X=1 About X=2 This problem has been solved!
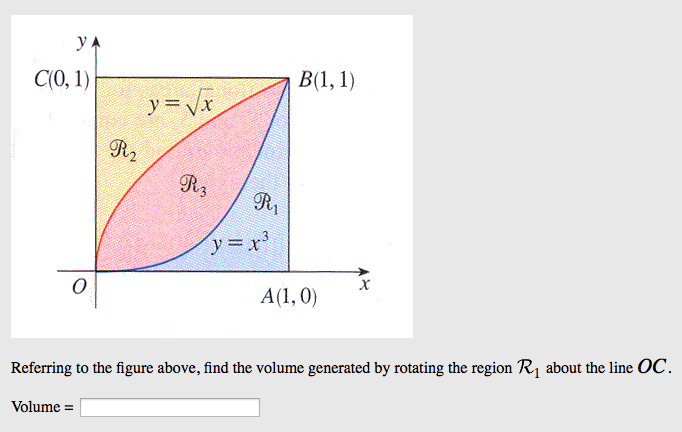


Using Disks Or Washers Find The Volume Of The Sol Chegg Com
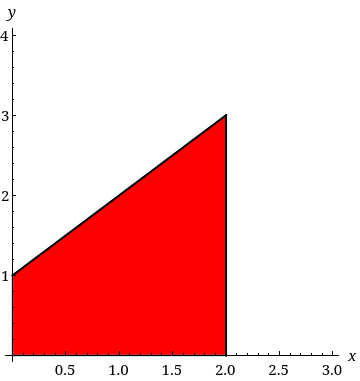


Find The Volume V Of The Solid Obtained By Rotating The Region Bounded By The Given Curves About The Specified Line Wyzant Ask An Expert
Jun 10, 17 · How do you use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by #y = x^3#, y=0 , x=1 revolved about the y=1?Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreBy y = x3, y = 0 and x = 2 about the xaxis y = 0, x = 1/2 and x = 2 about the yaxis Answer Since we're revolving around the yaxis, we can integrate in (disk, washer, shell) could you use to find the volume of the solid?


Part Two Confusion Regarding Calculus 2 Volumes Of Solids Of Revolution The Disk And Washer Method Askmath



Compute The Volume Of The Solid Obtained By Rotating The Region Enclosed By Y 1 X 2 Y 0 X 3 X 6 About The Line Y 1 Using The Method Of Disks Or Washers Via An
Jan 02, · C) Because we have to rotate about y=3, we find the radius by subtracting the functions from 3 and determine which function is the outer and innder radius with respect to the line y=3 The inner function would be y=x1 3 − ( x − 1) which gives, y = 4 − x and the outer function 3 − ( x 2 − 4 x 3) gives 4 x − x 2The points (x,y,z) of the sphere x 2 y 2 z 2 = 1, satisfying the condition x = 05, are a circle y 2 z 2 = 075 of radius on the plane x = 05 The inequality y ≤ 075 holds on an arc The length of the arc is 5/6 of the length of the circle, which is why the conditional probability is equal to 5/6This item 1/2 in x 2 in Plain Steel Plate Washer (100Piece) $1458 Everbilt 1/4 in Stainless Steel Flat Washer (6Pack) $118 Everbilt 1/2 in13 Galvanized Hex Nut (50Pack) $70 Product Overview Use the flat washer in an application using a bolt where 2pieces are being drawn together It provides a smaller outside Dia than a


Solved 1 1 Point Using Disks Or Washers Find The Volu Chegg Com



1 The Region R Is The Region Bounded By The Functions Y X 3 And X 1 Y 2 Find The Volume Homeworklib
About x = 2 more_vert Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified lineCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyAbout y = 1Find the volume of the solid obtained by rotating theregion bounded by the given curves about the specified line S


Solved The Volume Of The Solid Obtained By Rotating The R Chegg Com


4a Volume Of Solid Of Revolution By Integration Disk Method
Aug 04, 17 · Free Online Scientific Notation Calculator Solve advanced problems in Physics, Mathematics and Engineering Math Expression Renderer, Plots, Unit Converter, Equation Solver, Complex Numbers, Calculation HistoryCalculus Applications of Definite Integrals Determining the Volume of a Solid of Revolution 1 AnswerTative rectangle about the line y = −3, determine the volume of the representative washer, and then add them all up from x = 1 to x = 2 In Figure 3, the washer is drawn to the right The volume V w of the washer is given by V w = (area of the base)∆x where the base of the washer is the region formed by the two concentric circles V



Volume Of Revolution Disk Method


Volume Of A Solid Of Revolution
Question Find The General Solution Y' 1/x Y = 7/x^2 3 Xy' (1 2x^2)y = X^3 E^x^2 Y' (tan X)y = Cos X (x 2)(x 1) Y' (4x 3) Y = (x 2)^3 Y' (2 Sin X Cos X)y = E^sin^2 X Y' 4/x 1 Y = 1/(x 1)^5 Sin X/(x 1)^4 Xy' 2y = 2x^3 1 (1 X)y' 2y = Sin X/1 X X^2 Y' 3xy = E^x Solve The Initial Value Problem Y' 7y = E^3x, Y (0)


Volume Of A Solid Of Revolution Cylindrical Shells


Volume Of A Solid Of Revolution Disks And Washers



Washer Method Rotating Around Horizontal Line Not X Axis Part 1 Video Khan Academy


Volume Of A Solid Of Revolution Cylindrical Shells



Find Volume Of Region Bound By Y X Y X 2 Around X Axis Mathematics Stack Exchange


X Y 2 Y 2 X 0 About The Line Y 2 Youtube


12 4 Finding Volumes By Using Cylindrical Shells



How To Find The Volume Of The Region Bounded By Y X 2 Y 4 And The Y Axis For X 0 Rotating The Region Around The X Axis Quora
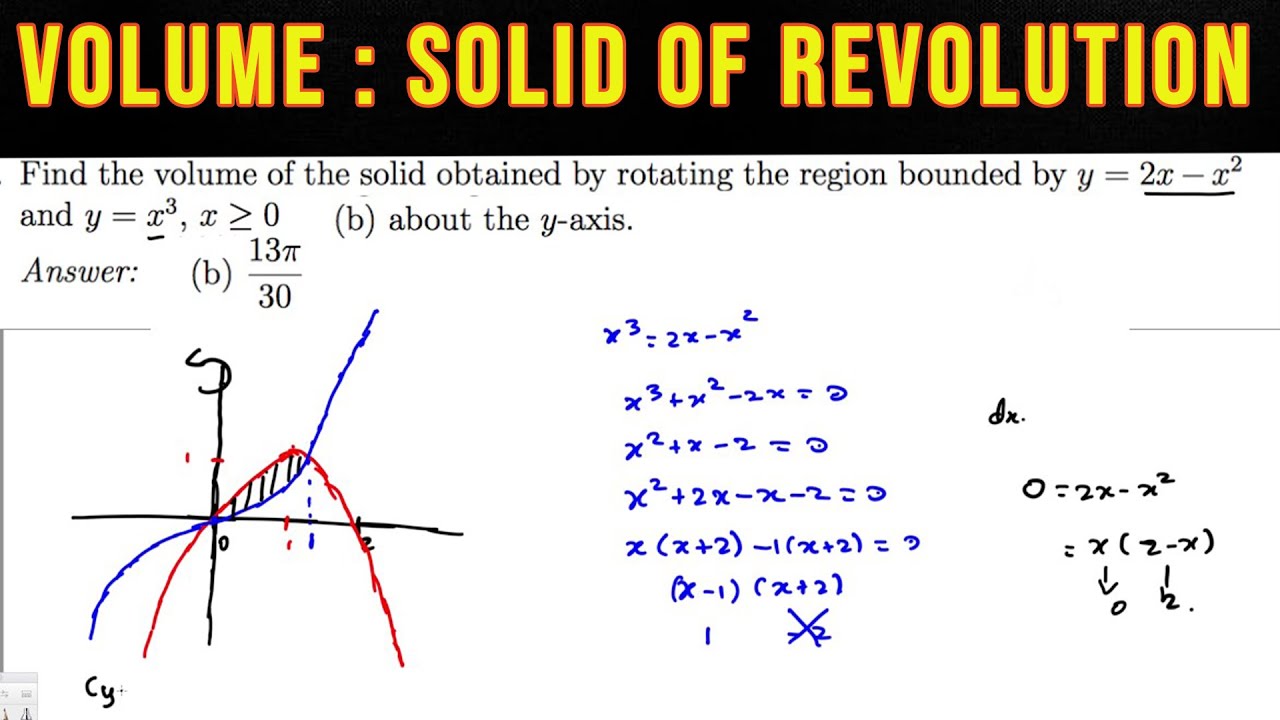


Find The Volume Of The Solid Obtained By Rotating The Region Bounded By Y 2x X2 The Line X Youtube
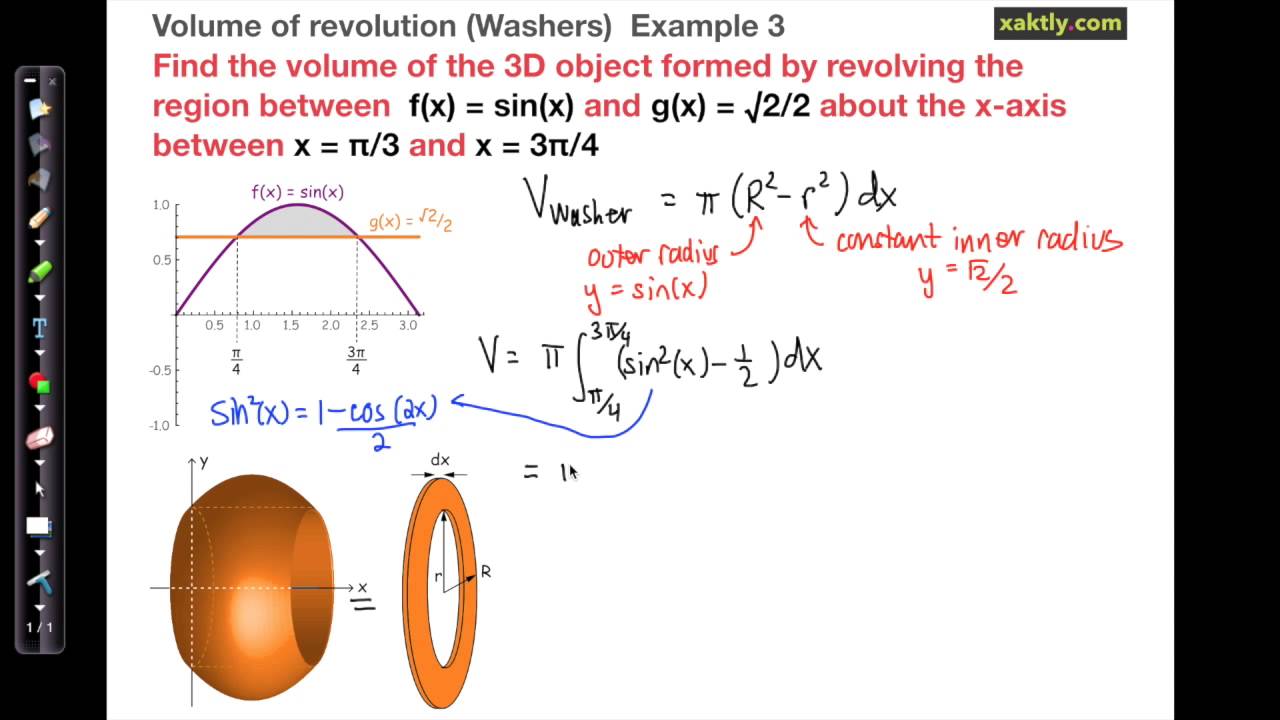


Volume By Washers



Find The Volume V Of The Solid Obtained By Rotating The Region Bounded By The Given Curves About The Specified Line 8x Homeworklib



Rotate The Region Bounded By The Curves Y Sqrt 4 X 2 X 0 Y 0 About The Y Axis Find The Volume Youtube
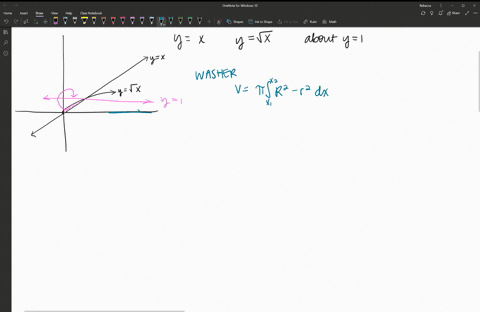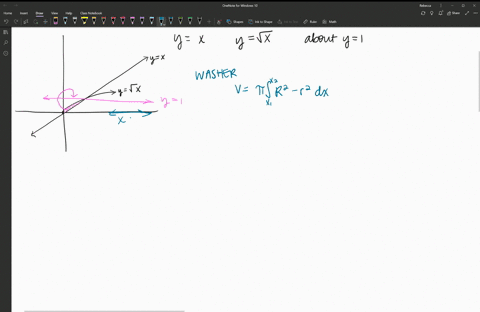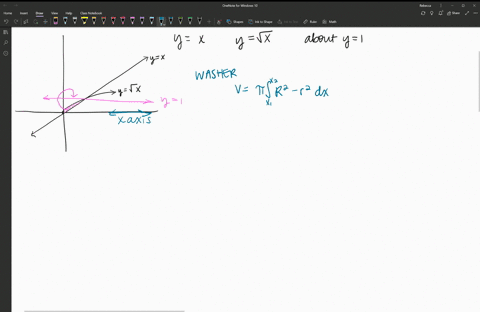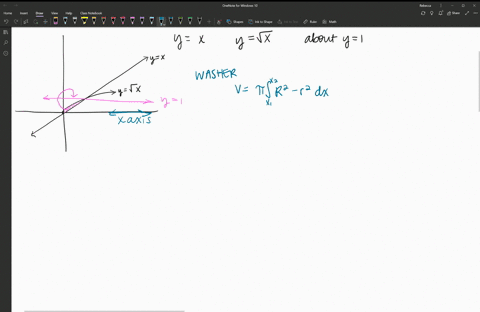


Applications Of Integration Essential Calculus



Do Now Find The Volume Of The Solid Generated When The Ppt Video Online Download


Volume Of A Solid Of Revolution Cylindrical Shells
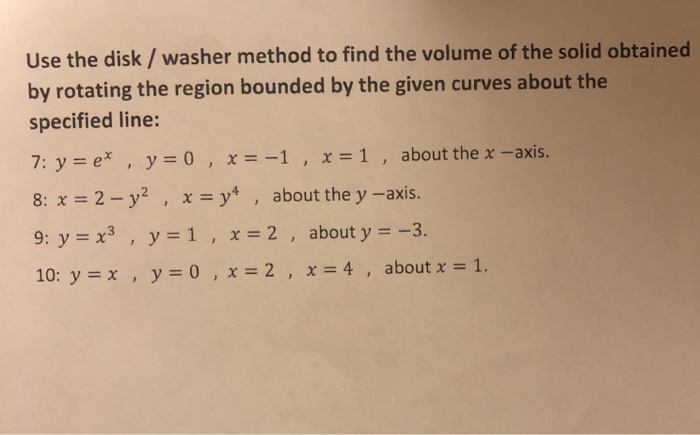


Solved Use The Disk Washer Method To Find The Volume Of Chegg Com


4a Volume Of Solid Of Revolution By Integration Disk Method



Answered 1 Find The Area Bounded By The Bartleby


Volume Of A Solid Of Revolution Disks And Washers
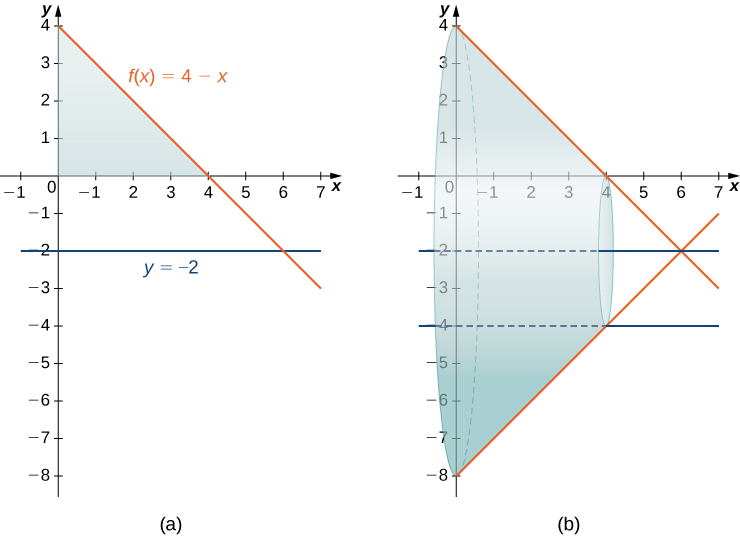


6 2 Determining Volumes By Slicing Calculus Volume 1


Volume Of A Solid Of Revolution Cylindrical Shells


4a Volume Of Solid Of Revolution By Integration Disk Method
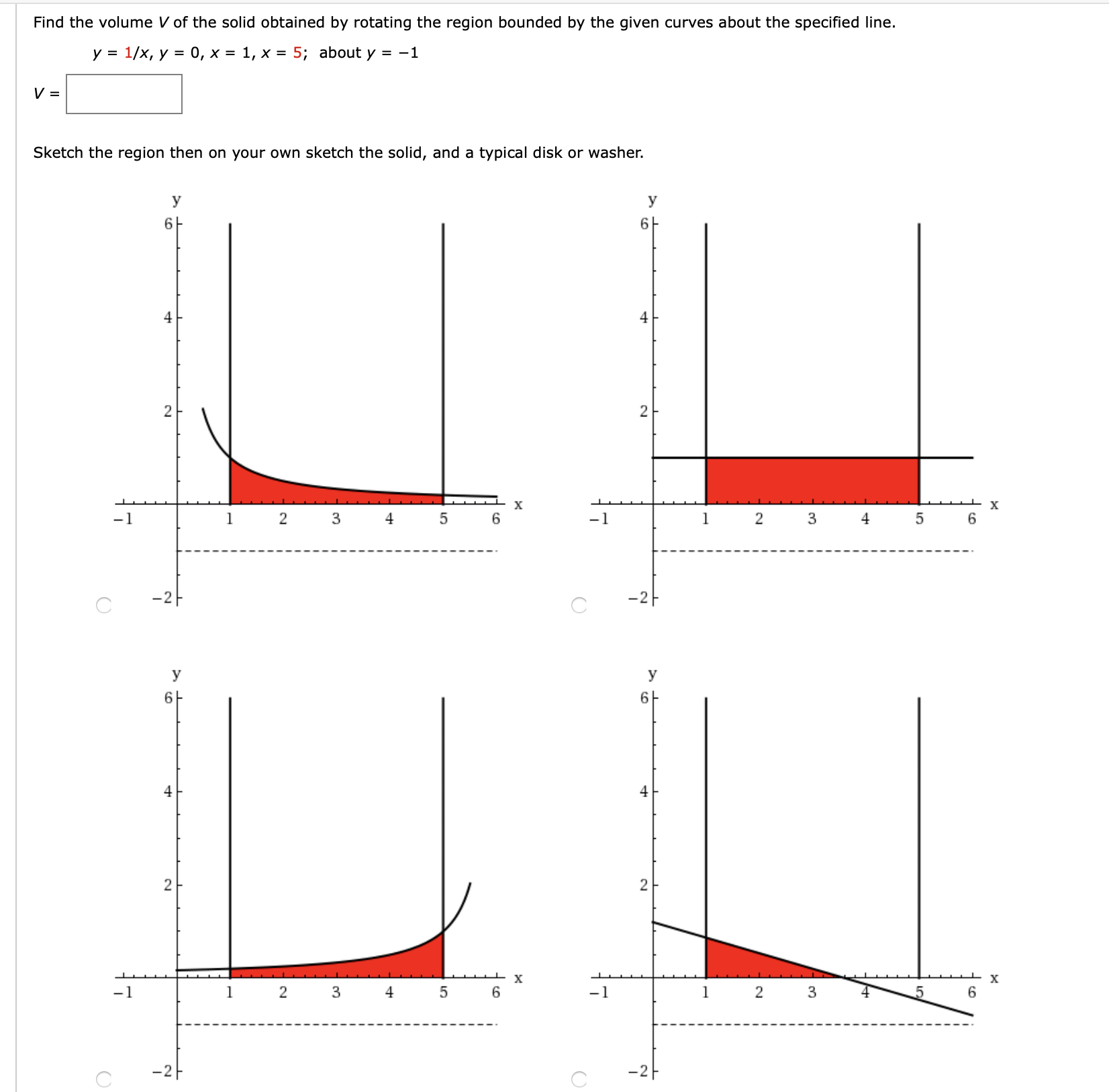


Answered Find The Volume V Of The Solid Obtained Bartleby
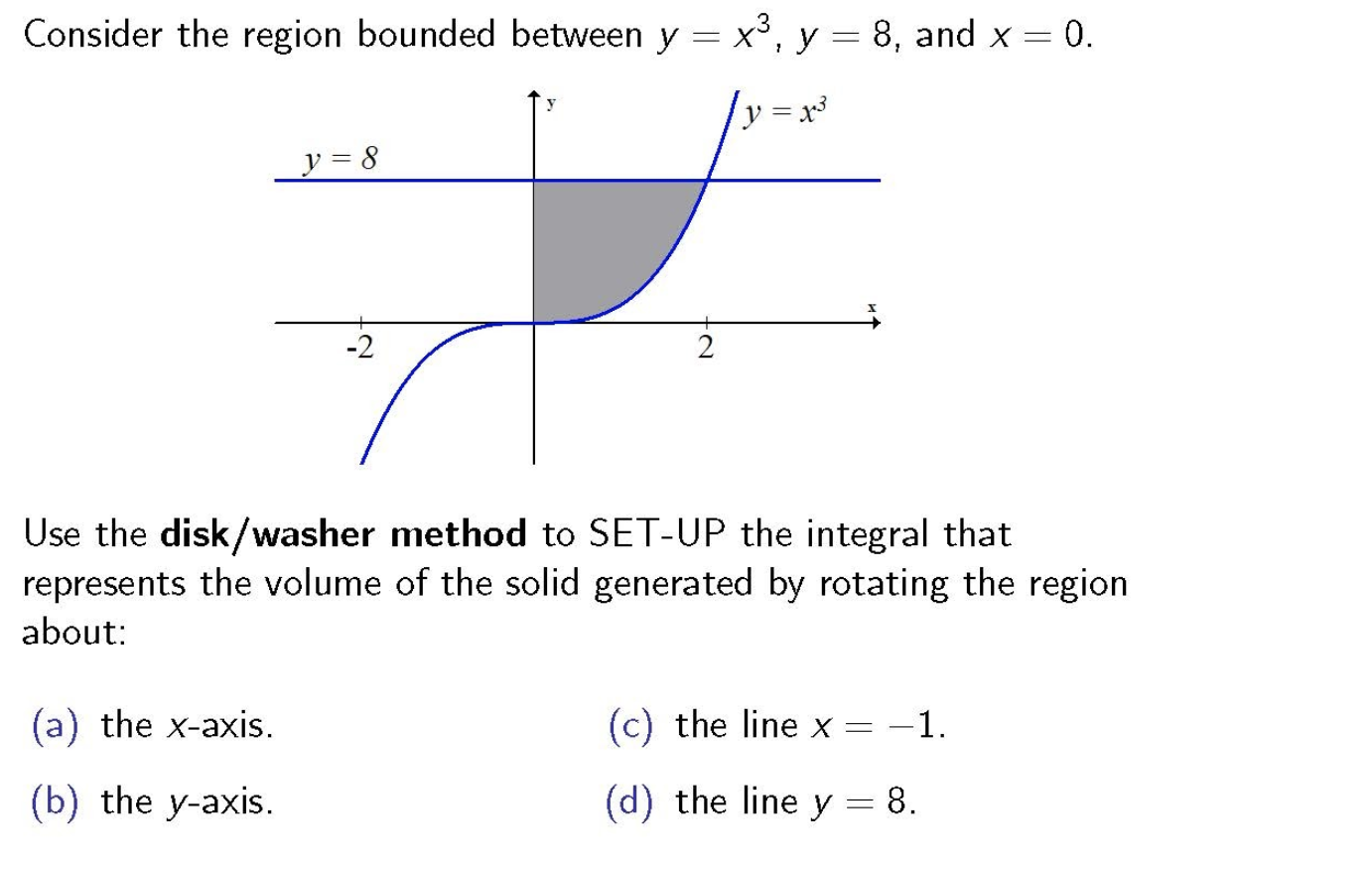


Answered Consider The Region Bounded Between Y Bartleby



How Do You Find The Volume Of The Solid Obtained By Rotating The Region Bounded By The Given Curves About The Specified Line Y X Y Sqrt X About X 2 Socratic



Volume Of Revolution Disk Method



Solved 1 The Volume Of The Solid Obtained By Rotating Th Chegg Com


Volume Of A Solid Of Revolution Disks And Washers



Volume Of Revolution The Washer Method Not About The X Or Y Axis Youtube
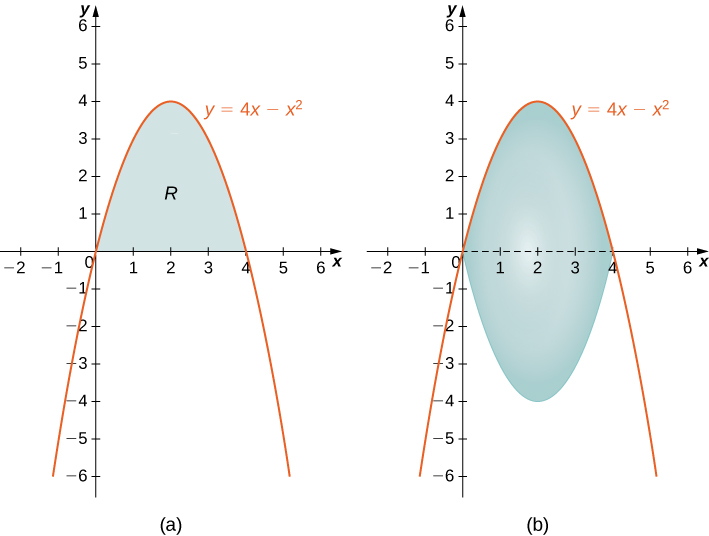


6 3 Volumes Of Revolution Cylindrical Shells Calculus Volume 1
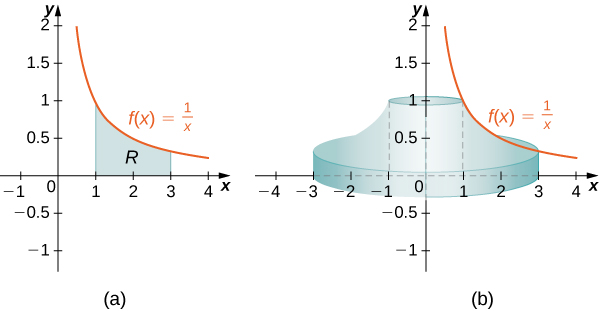


6 3 Volumes Of Revolution Cylindrical Shells Calculus Volume 1


4a Volume Of Solid Of Revolution By Integration Disk Method
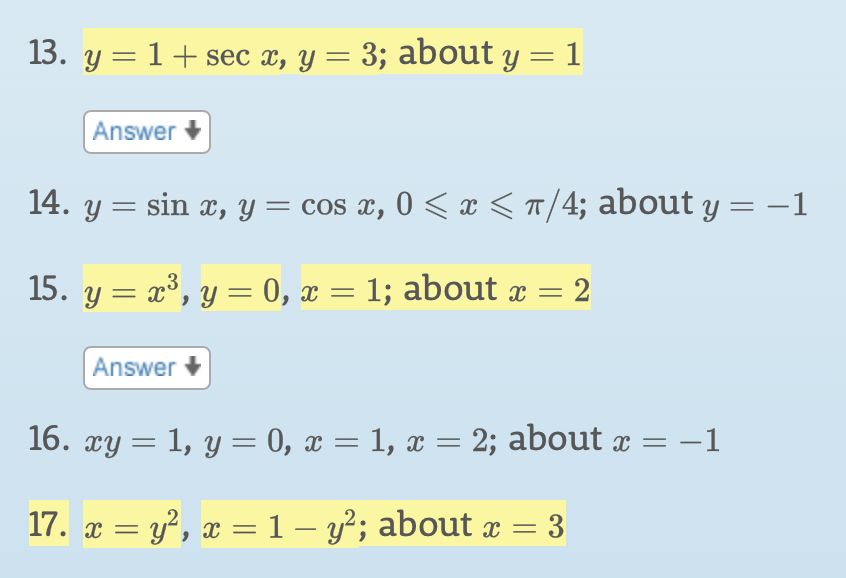


Solved Find The Volume Of The Solid Obtained By Rotating Chegg Com


Volume Of A Solid Of Revolution Disks And Washers
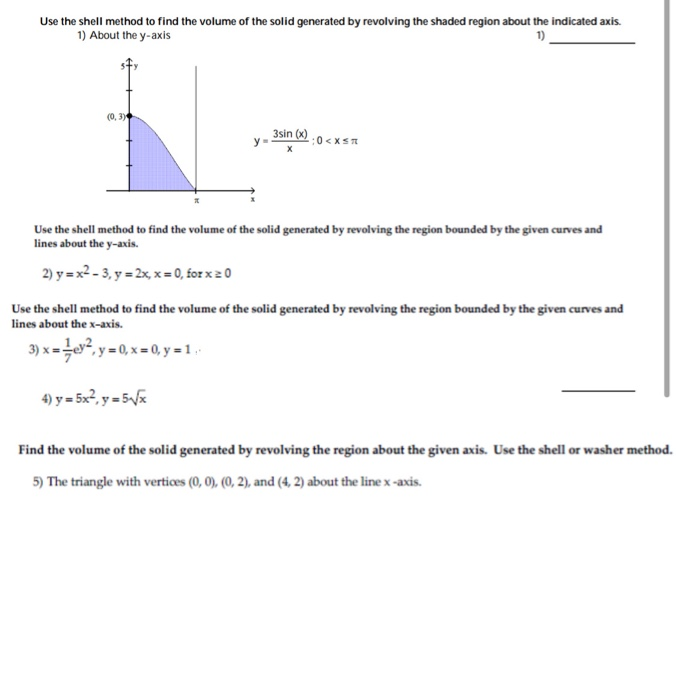


Solved Use The Shell Method To Find The Volume Of The Sol Chegg Com



How Do You Find The Volume Of The Solid Generated By Revolving The Region Bounded By The Graphs Y 2x 2 Y 0 X 2 About The X Axis Y Axis The Line Y 8 The Line X 2
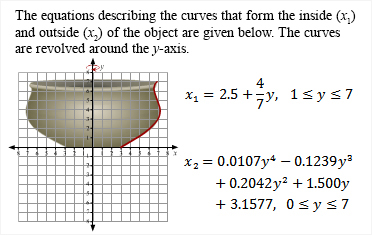


Volumes Of Revolution
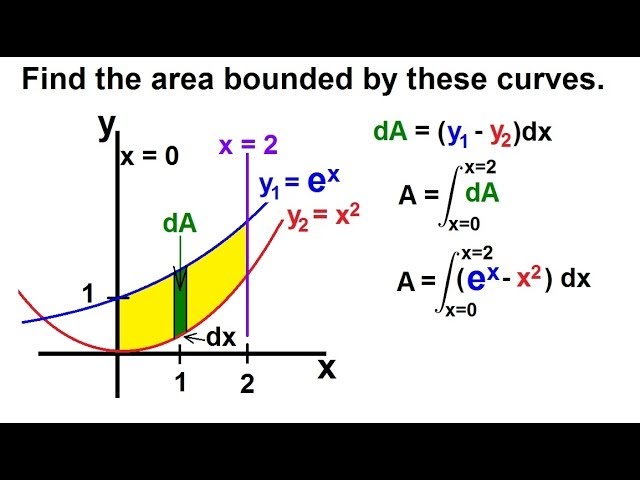


Calculus 2 Integration Finding The Area Between Curves 1 Of 22 Ex 1 Y E X Y X 2 X 0 X 2 Youtube


Volume Of A Solid Of Revolution
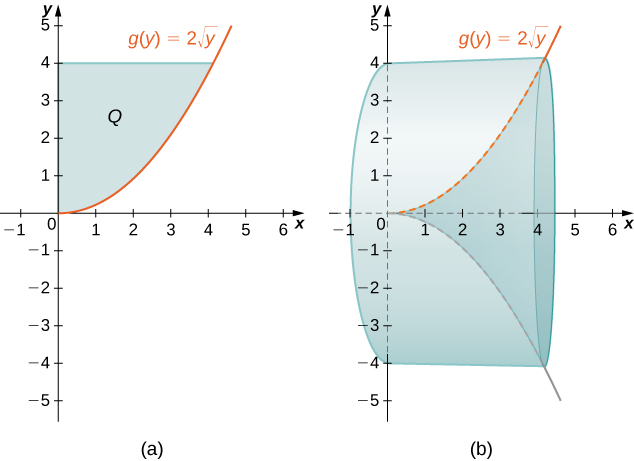


6 3 Volumes Of Revolution Cylindrical Shells Calculus Volume 1



What Is The Area Of The Region Bounded By The Parabola Y 2 4x And The Line X 1 Quora
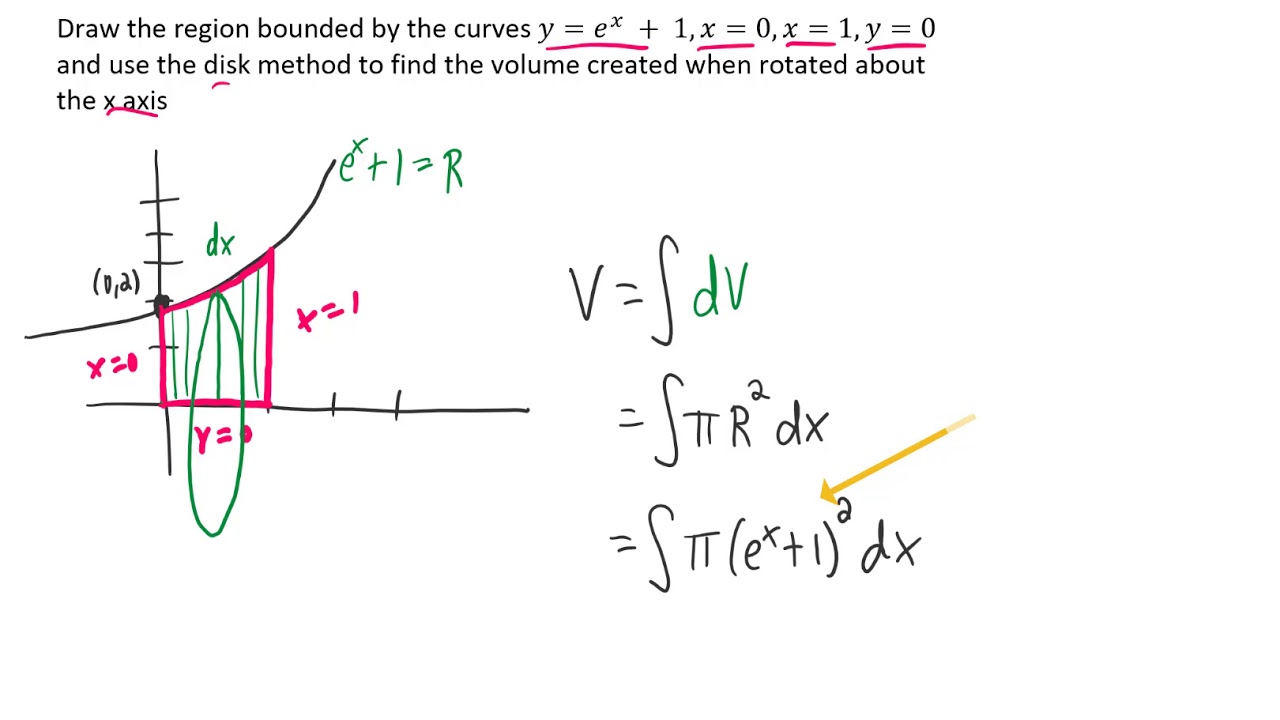


Draw The Region Bounded By The Curves Y E X 1 X 0 X 1 Y 0 And Use The Disk Method To Find The Youtube



A Using Disks Or Washers Find The Volume Of The Solid Obtained By Rotating The Region Bounded By The Curves Y X 2 3 X 1 And Y 0 About The


What Is The Volume Of The Solid Formed By Rotating The Region Inside The First Quadrant Enclosed By Y X 2 And Y 5x About The X Axis Quora
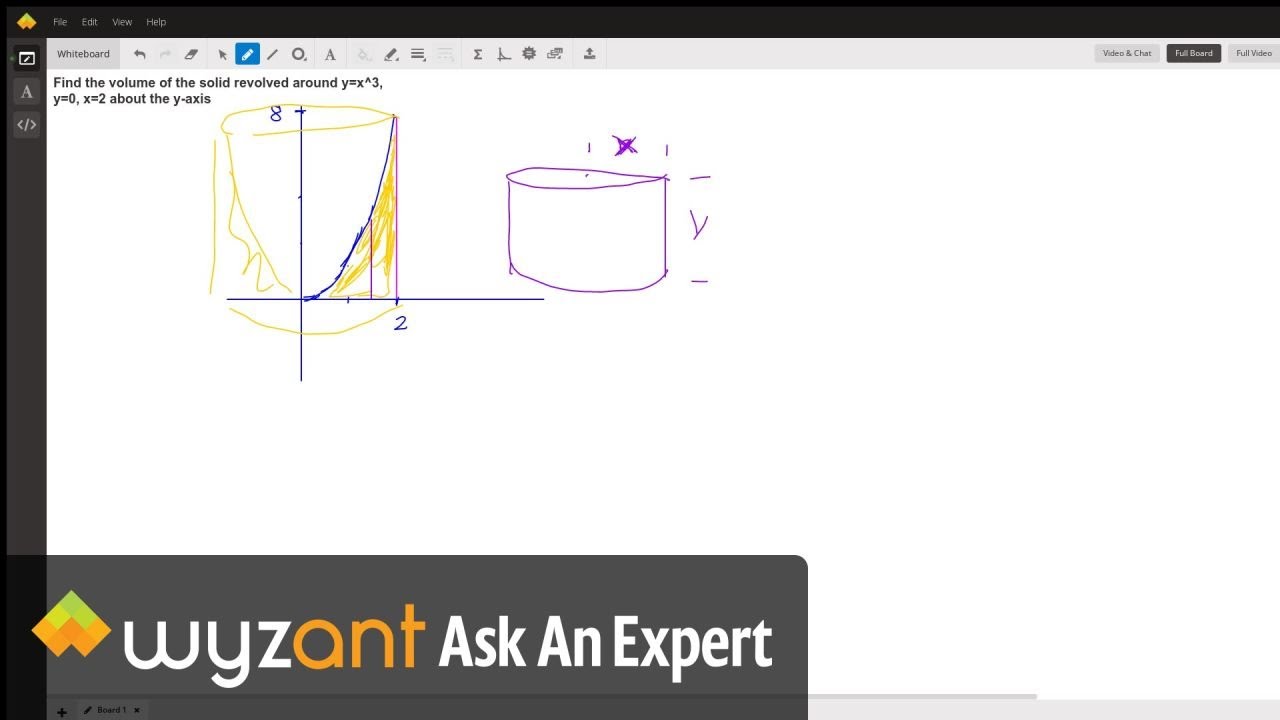


Find The Volume Of The Solid Revolved Around Y X 3 Y 0 X 2 About The Y Axis Wyzant Ask An Expert
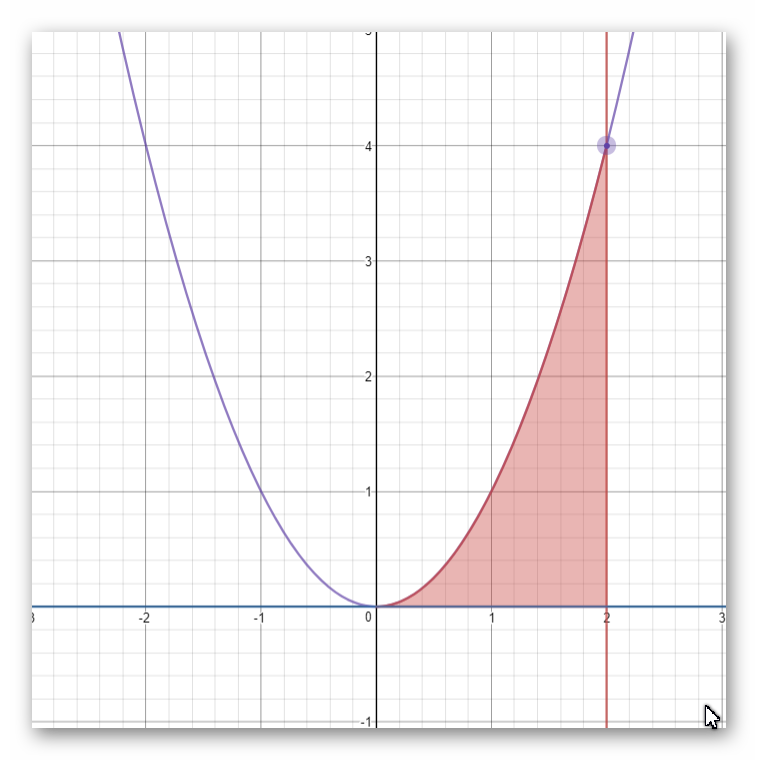


How Do I Find The Volume Of The Solid Generated By Revolving The Region Bounded By Y X 2 Y 0 And X 2 About The X Axis The Y Axis Socratic
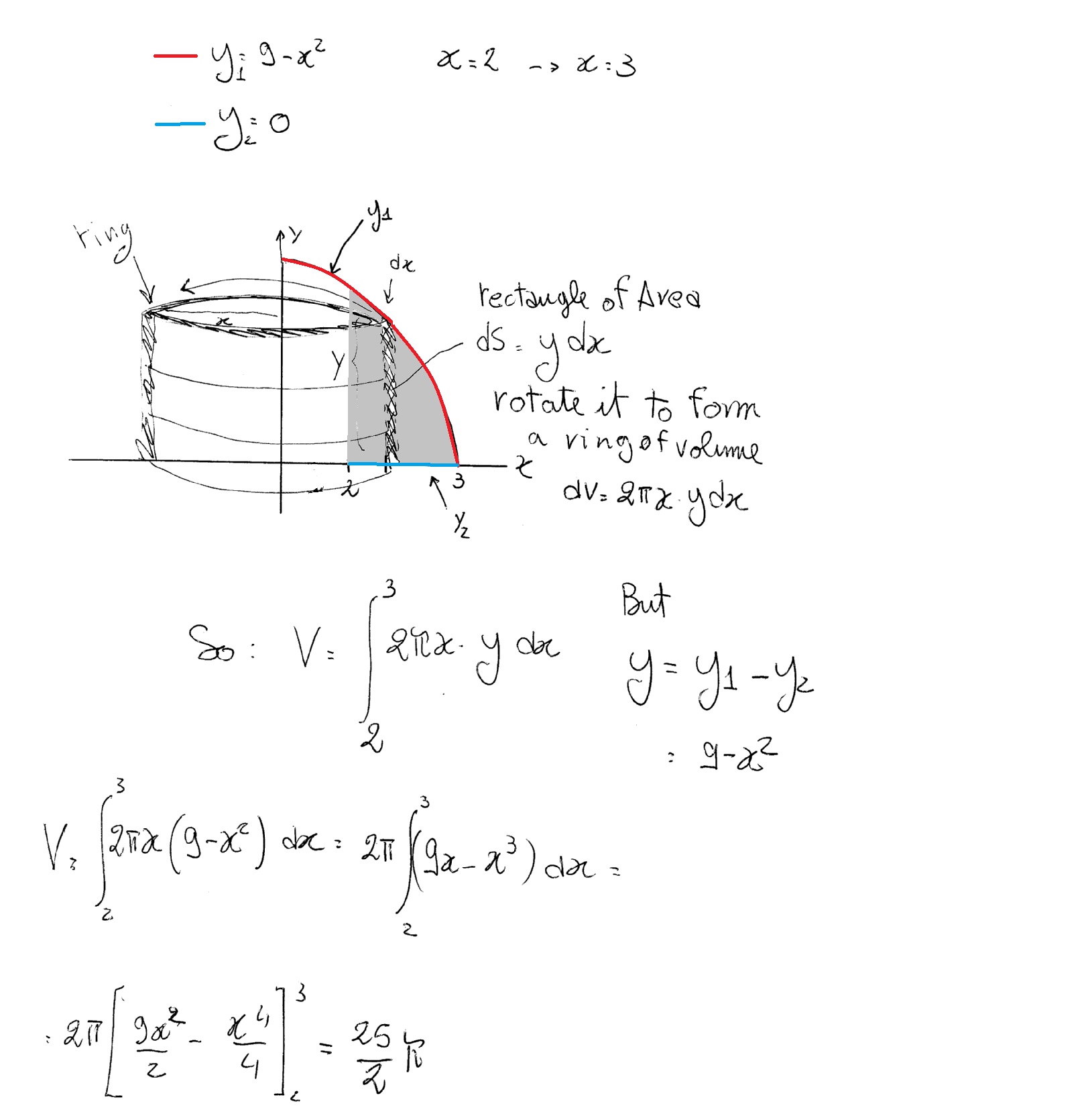


How Do You Find The Volume Of The Solid Generated By Revolving The Region Bounded By The Graphs Y 9 X 2 Y 0 X 2 X 3 About The Y Axis Socratic
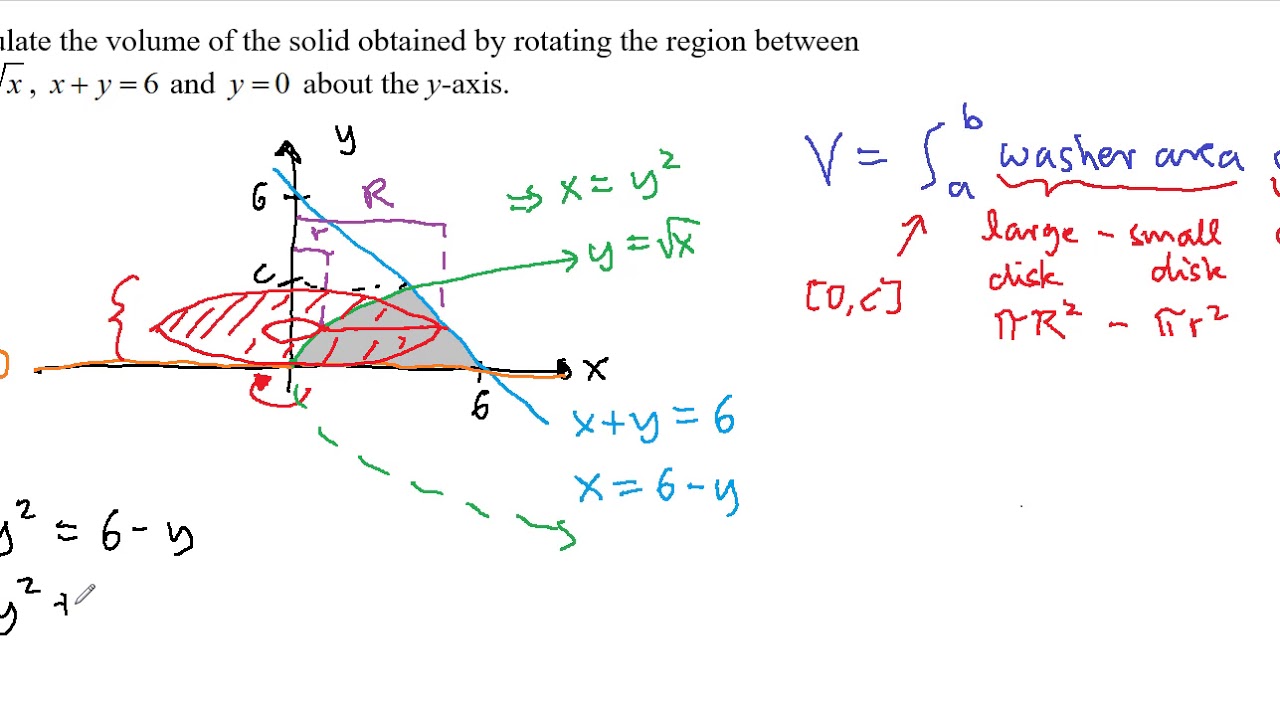


Volume Of Revolution Disk Method
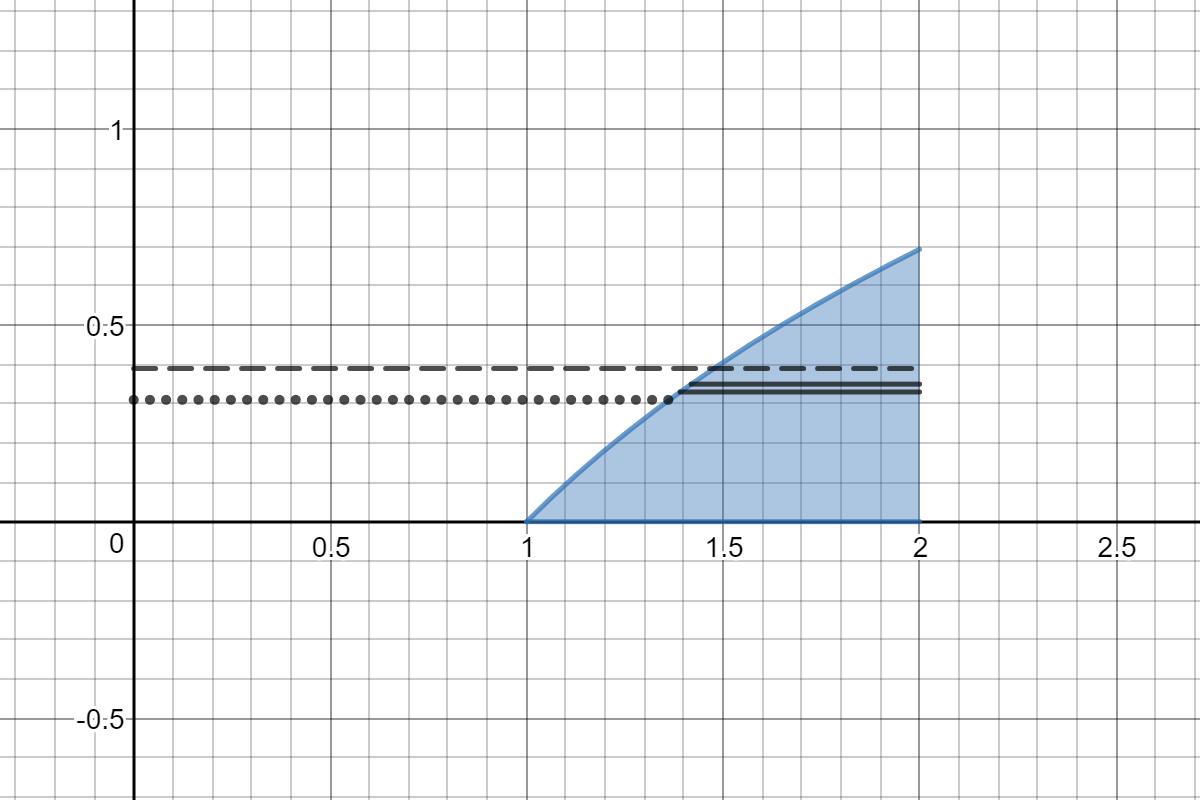


How Do You Find The Volume Bounded By Y Ln X And The Lines Y 0 X 2 Revolved About The Y Axis Socratic
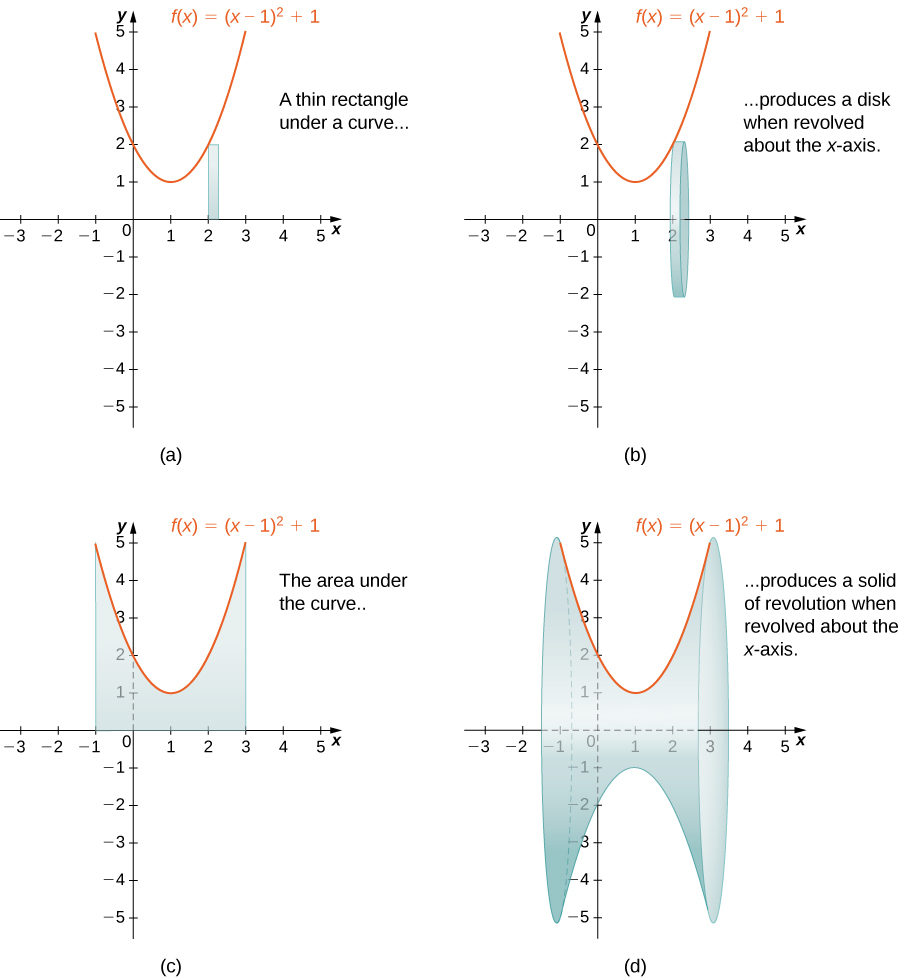


6 2 Determining Volumes By Slicing Calculus Volume 1


4a Volume Of Solid Of Revolution By Integration Disk Method
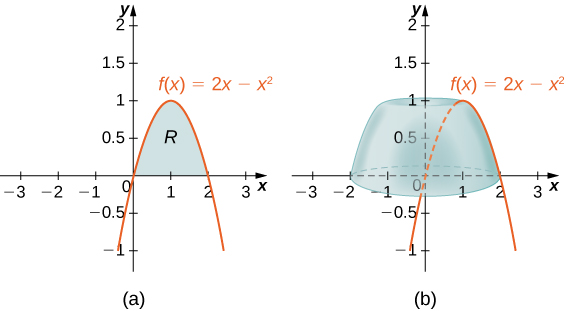


6 3 Volumes Of Revolution Cylindrical Shells Calculus Volume 1


Solved Find The Volume Of The Solid Obtained By R



Volume Of Revolution Worksheet Doc Volume Area


4a Volume Of Solid Of Revolution By Integration Disk Method


6 2 Determining Volumes By Slicing Calculus Volume 1



0 件のコメント:
コメントを投稿