三角形 三角形の合同条件 三角形の合同条件2 三角形の合同の証明 基本問題1 三角形合同の証明1 三角形の合同証明2 三角形の合同証明3 三角形の合同証明4 三角形の合同証明5 平行線の証明 三角形の合同証明6 二等辺三角形 二等辺三角形の性質 二等辺三角形2 直角三角形1 直角三角形2 直角三角形3 三角形証明(発展1) 三角形の証明(発展2) 三角形の証明(発展3) 中3数学 3分でわかる!円周角の定理とはなんだろう?? 中2数学 中2数学一次関数の傾きがわかる2つの求め方 中3数学 平行線にはさまれた線分の比の2つの証明 中1数学 ヒストグラムを使った平均値の求め方がわかる4ステップ3変化の割合 62次関数と三角形の面積 3乗法の公式 8式の計算の利用 1平方根とは?

三平方の定理について考える4 三角形の相似を使った証明方法 身勝手な主張
中 3 数学 証明 問題
中 3 数学 証明 問題-このことを証明しなさい。 練習問題2 連続する2つの奇数の積に1をたすと、その2つの奇数の間の偶数の2乗になる。 このことを証明しなさい。 練習問題3 連続する3つの自然数の真ん中の数の2乗から1をひくと、その他の2つの数の積になる。文字を使って、式をつくり、計算を進めればいいんだね。 証明するのは、 「偶数と奇数の和は奇数になる」 だから、この部分を式にしよう。 (偶数)+(奇数)=(奇数) だね。 偶数と奇数は、いま2m、2n-1とおいているから、 (偶数)+(奇数) =2m+(2n-1) =2m+2n-1 =



数学 中学証明問題を解く4つのポイント
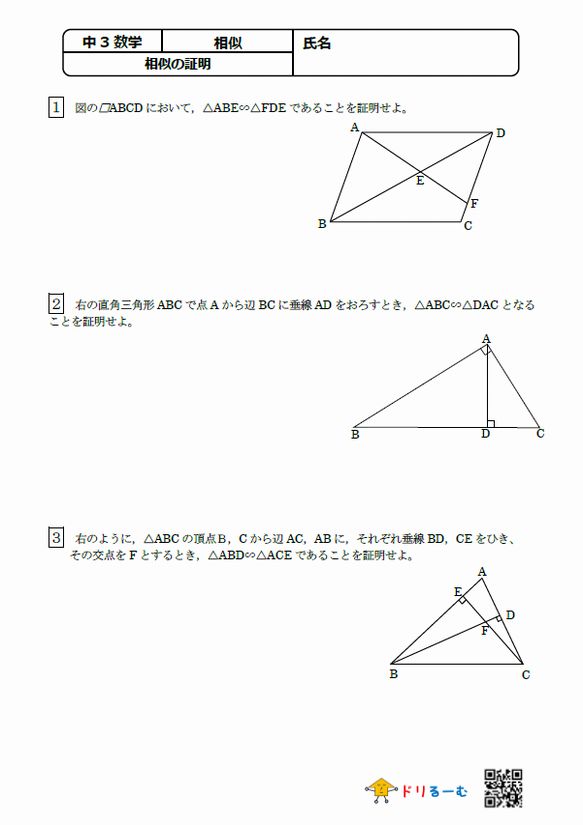
相似の証明の簡単な問題が載っけてあります! 答えは丁寧に書かれているのでいらないところは、省略してください (答えは後半にあります) 学年 中学3年生, 教科書 未来へひろがる数学3 啓林館, 単元 図形と相似, キーワード 数学,相似の証明,相似,math動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru中3 数学 式の計算 J 証明 宿題プリント 解答 J1 まん中の数をnとすると、連続する3つの整数は、n1, n, n1となる。 (n1)(n1)1=n2 11=n2 よって、最大の数と最小の数の積に1を加えた数は、まん中の2乗に等しい。
3 ab=ac, ad=aeのとき abe≡ acdとなることを証明しなさい。 4 「数学。証明問題、解き方と記述のコツ!その1」の中で、 証明問題は3ステップの順番で 問題に取り組むというお話をしました。 今回はその続きで、 ステップ3の ③証明の記述を行っていく からお中3です。「平方根」の変形のコツは? 中3です。「平方根」の変形の応用問題が。 中3です。「平方根」の近似値を使う問題が。 中3です。「平方根の近似値」、応用問題が。 中3です。「2乗に比例する関数」の"変化の割合"は? 中3です。2平方根の大小と近似値 中3 数学 1式の計算 2平方根 32次方程式 4関数 中3数学
校数学では,証明は高等学校の幾何の指導内容とされ ていました。中学校の数学では,図形の性質の学習に おいて,性質の成り立つわけを「説明」する内容が3 年生にありました。 「証明」という用語が,戦後の中学校の教科書に登 場したのは,昭和30 テーマ: 実力テスト数学 リロード推奨 ~高校入試までの流れ~ 2月3学期期末テスト 3月中2学年末試験 4月第1回実力テスト (1年の範囲) 5月1学期中間テスト,第2回実力テスト(2年の範囲) 6月期末テスト *問題は追加していく予定です。多項式の計算 多項式と単項式の乗除 乗法公式 式の展開と加法、減法 因数分解の基本 因数分解ーいろいろな計算 因数分解 係数の組み合わせ 計算の工夫 素因数分解多項式の計算の利用 式による証明 図形への利用多項式の計算のまとめ まとめの問題平方根




数学 中3 13 式の計算の利用 数字の証明編 Youtube



Studydoctor三角形の合同証明の進め方 中2数学 Studydoctor
中3数学 図でよくわかる三平方の定理(ピタゴラスの定理)の証明と計算問題 を三平方の定理(ピタゴラスの定理)という。 直角三角形に関する定理で、斜辺の二乗が残りの辺の二乗の和に等しい。 今回は"証明のやり方"についてまとめました! 今、相似な図形の証明をやっているのでそれのための復習で作りました! 学年 中学2年生, 教科書 未来へひろがる数学2 啓林館, 単元 証明, キーワード 証明,証明のやり方,定義,定理,合同条件,みそはた証明を書いていこう! では、頭の中でみちびけた事を、証明の文章にしていこう。 3ステップを意識すると書きやすいんだったね。 POINT まずはステップ1注目する図形 今回テーマになっているのは、図の円だね。 「~において」と書き出そう。 証明の書き方の例 次にステップ2等しい弧



中3数学 式の利用 整数の証明問題の定期テスト対策予想問題 Atstudier



中学数学 証明問題のやり方は 解き方のコツや図形問題への対処法を解説 学びtimes
中3数学の「式の計算の利用(連続する整数の性質の証明)」についてまとめています。 よく出題される出題パターンの1つです。 しっかりりおさえていきましょう。 それでは、中3数学の「式の計算の利用(連続する整数の性質の証明)」です。 目次 連続する整数の表し方 倍数や割り切れることの証明の流れ 等しいことの証明の証明の流れ 連続する整数の性質数学の証明が驚くほどできるようになる4つのコツ! 証明問題は避けて通れないが、苦手とする受験生は多い。 普通に方程式を解いたり、積分をしたりといった計算は得意なのに、証明問題になると急に手こずってしまうのだ。 自分で方針を立て、論理をわかりやすく説明する。 そのためには、 計算力や思考力以外の力 が必要である。 そして、その力は数日で中3数学三平方の定理 三平方の定理の証明 三角形の2辺の長さから残りの1辺の長さを求める方法について学習します。 三角定規の3辺の比




中3数学 証明で使える定理まとめ 中学生 数学のノート Clear



中2数学 通年用問題集 8章 合同の証明演習
今回は中3で学習する式の計算の利用から 「円、正方形の図形に関する証明」 を解説していきます。 取り上げるのは、こういった図形の問題です。 中3 相似な図形と証明 カテゴリーの記事一覧 すべて無料! 星組の中学数学講座 授業動画は声と手だけ、テキストは下手な字で手書きの低クオリティー! だけど、内容は役に立つと思います。 また、無料学習プリント集としてもお使いいただけます多項式・因数分解の利用(2)証明問題 ~中学3年生の数学~ このページは『多項式・式の計算の利用』‥一般的に言う応用問題の中の証明問題 (文章問題)の解説になります。 証明には型のような手順がありますので覚えていってくださいね! 1 多項式




中学3年 数学 東京書籍 新しい数学 相似な図形 平行線と比 赤城 ᐡᐤᐡ
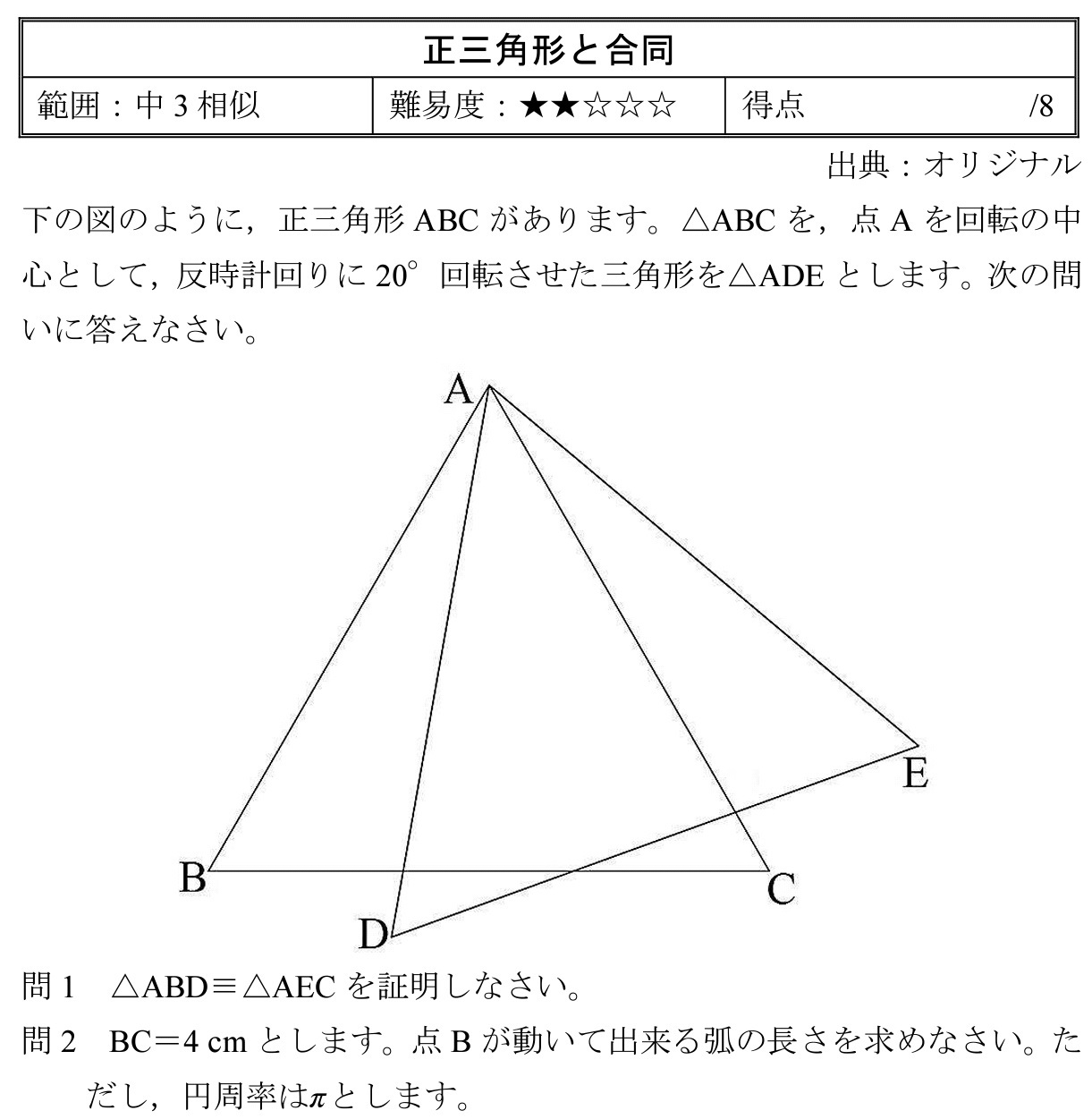



訂正 正三角形と合同 高校入試 数学 良問 難問
例) 連続する3つの整数の和が3の倍数になることの証明 nを整数とすると 連続する3つの整数は n1, n , n1 と表せる。 ← n,n1,n2で表してもよい (n1)n (n1)=3n nは整数だから3nは3の倍数 よって 連続する3つの整数の和が3の倍数になる中3数学 2次関数の利用・相似な図形の利用・相似比 3学期期始めテスト・期末テスト用 中学3年数学 年2学期中間テスト 2次方程式の利用 お絵かきできるかな? 中3数学 簡単証明乗法の公式はなぜ使えるんだろう?? 中3数学 1655 素因数分解の応用問題の解き方がわかる3つのステップ 中2数学 文字式の利用連続する3つの整数の和が3の倍数になる証明 中3数学 16




無料 中3数学 基本問題 解答プリント 図形の相似2 相似条件と証明




数学 中3 48 相似の証明チャレンジ Lv 3 Youtube
中3数学コースの特徴 代数・幾何・確率・整数論の各分野の学習を通じて、数学の楽しみをみなさんに伝えることが私達の使命です。 そのために生徒のみなさんには、例えば、次のようなことに挑戦してもらいます。 (1) 春期講習では、起こりやすさを 中3数学 式の計算の利用(数に関する証明)まとめと問題 入試問題でもよく出題される「式の計算の利用」、その中でも数に関する証明問題について今回取り上げました。 「2つの連続する偶数が」「3つの連続する数を」「2つの奇数の積から」などいろんなパターンがありますが、どのように式を立てたら良いかわからなくなる、と混乱しやすいところです 中3社会は「中間テストの復習」を行い、「高度成長」や「沖縄返還」を教えました。 中3数学は「中間テストの復習」を行い、「文字式による証明」を教えました。 中間テスト、よくできて良かったですね。 さて、「文字式による証明」です。



中学 数学の証明問題です 超難問 1 から全然わかりません 今まで見た中 Yahoo 知恵袋




超 パワーアップ中学数学 図形の証明 中継点 文字式の表現 活用テクニック Myisbn デザインエッグ社 長通 幸大 本 通販 Amazon
などと疑問をお持ちの方もいるでしょう。 数学の証明問題のやり方がわからないという中学生は非常に多いです。 しかし、 解き方のコツさえ覚えれば、中学生で習う証明問題はそれほど難しくありません 。 今回は中学生の証明問題のやり方について、解き方のコツや図形問題への対処法などを解説します。 これを読めば、難しく思われた証明問題が簡単に解ける動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaruこのブログは「高校入試 難問」や「高校入試 数学 良問」などで検索して来られる方が多いです。 ということで,久々に芸術的な,中学数学の問題をご紹介します。 今回は, 14年度大阪府Bの問題 です。 えげつない問題もあるのですが,中には計算は



1



数学の証明問題の解き方がわかる4つのステップ Qikeru 学びを楽しくわかりやすく
FdData 中間期末:中学数学3 年:相似 相似な図形/三角形の相似条件/相似の証明:2 辺の比とその間の角/2 組の角が等しい/ 直角三角形など /三角形の相似と長さ/FdData 中間期末製品版のご2次関数② 曲線 (2次式の求め方) 直線 (一次式の求め方1) 直線 (一次式の求め方2) 直線 (一次式の求め方3) 直線 (一次式の求め方4) 面積の問題 (基) 面積の問題 (標) 交点の座標相似の証明1 図の ABCは∠BAC=90°の直角三角形である。 頂点Aから辺BCに垂線を下ろしその交点をDとする。 A B C D ABD∽ CBAを証明せよ。



Studydoctor三角形の合同の証明 応用 中2数学 Studydoctor




中3数学基礎 本当に使える裏技 相似の問題で差をつけろ 定期テストや高校入試に レオンの中学数学探検所
中学3年生 数学 円周角の定理 練習問題プリント 円周角と中心角の関係や、それを証明する方法を理解し、円周角の定理を活用する問題を繰り返し練習します。




三平方の定理について考える4 三角形の相似を使った証明方法 身勝手な主張




中2数学 証明とは 練習編 映像授業のtry It トライイット
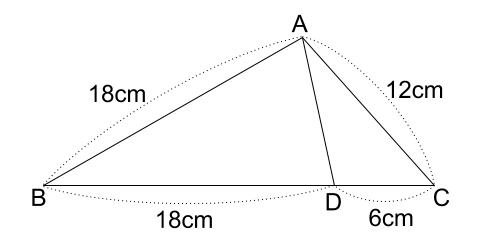



中学数学 相似の証明 その1 中学数学の無料オンライン学習サイトchu Su




苦手な人が多い図形の証明問題を解くコツを解説 実は非常に簡単なんです 学習塾 Step By Step



中2数学 発展問題プリント12 図形6 証明のしくみと根拠 問題 226




ひらめきに頼らず中学数学の図形問題を解く7つのコツ




この証明問題の答えの 仮説 Clear




中3数学 式による説明 整数の証明のポイントと練習問題




中3数学 図形と相似9 相似条件と証明 折り返しの図形 すべて無料 星組の中学数学講座
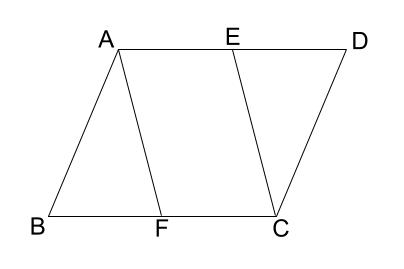



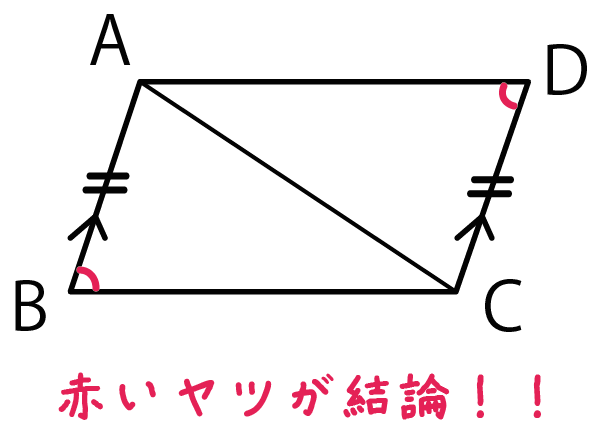
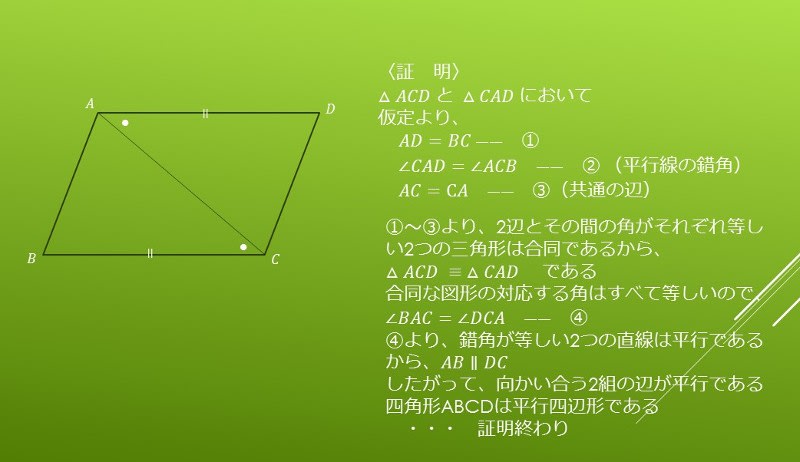
中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su




中2 中2 数学 5章 図形の性質と証明 プレイカラー 中学生 数学のノート Clear



数学の先生でも解けない 超 難問 悔しかったら解いてみろ 問 Xの角 Yahoo 知恵袋
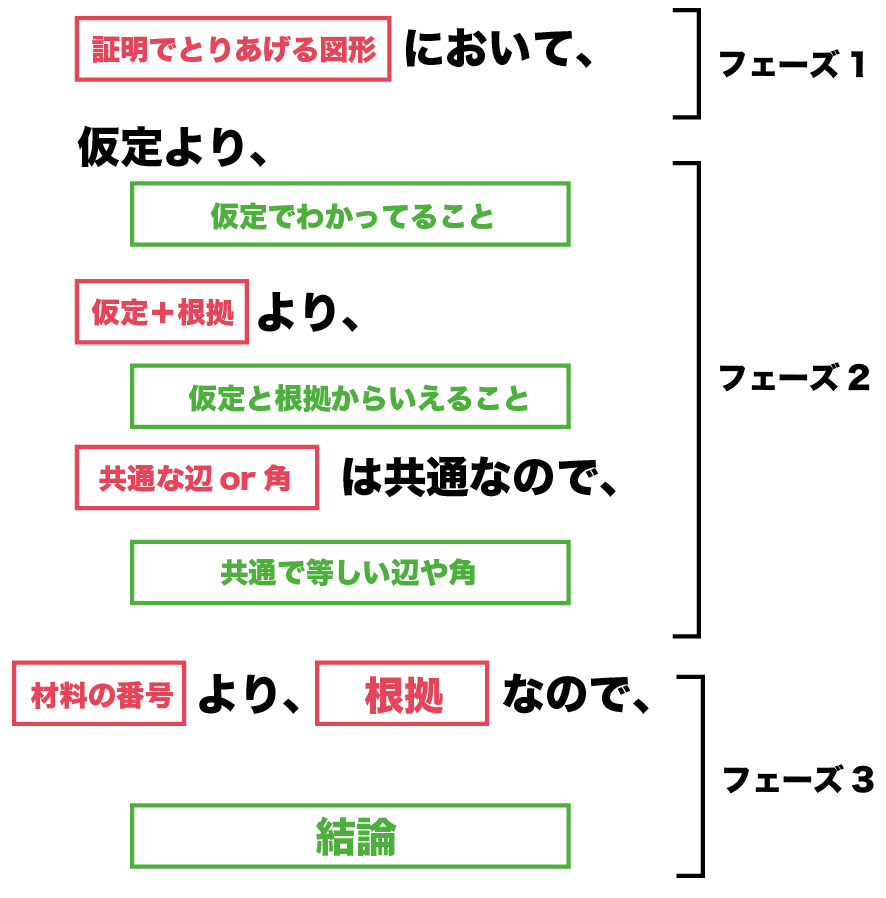



中学数学 3年間つかえる証明問題の書き方 Qikeru 学びを楽しくわかりやすく



1




中学2年数学練習問題 図形の合同と証明の定期テスト対策問題



中2数学 図形の証明問題では様々な図形の性質を理解することが大切 中学生 受験対応 英語 数学 学習講座
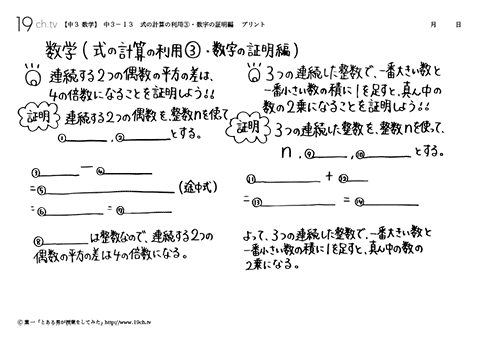



中学3年の数学 動画 式の計算の利用 数字の証明編の問題 19ch
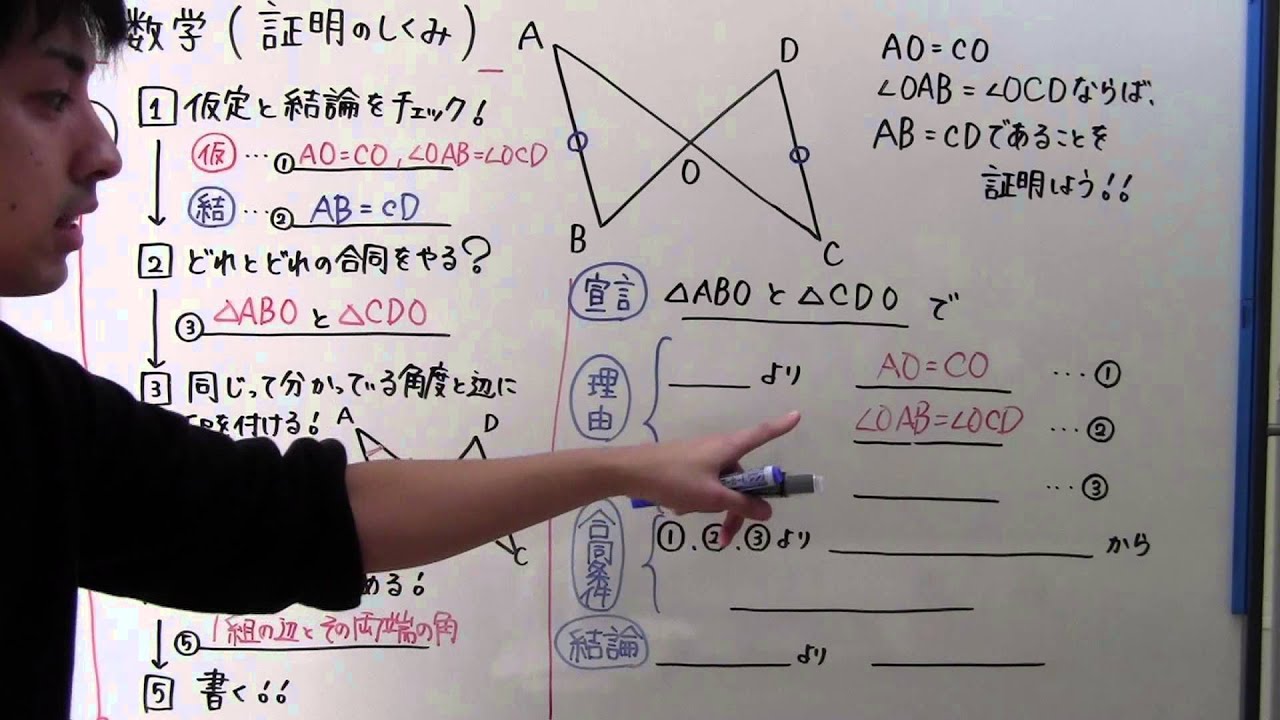



中2 数学 中2 60 証明のしくみ Youtube




式の計算 式による図形の証明問題の解き方のコツ 中学数学 定期テスト対策サイト




世界一わかりやすい数学問題集中2 5章 図形の性質と証明



働きアリ 数学科




中学数学 証明 証明が苦手な中学生さんへ 家庭教師が教えるコツとポイント 新潟の家庭教師 ホームティーチャーズ
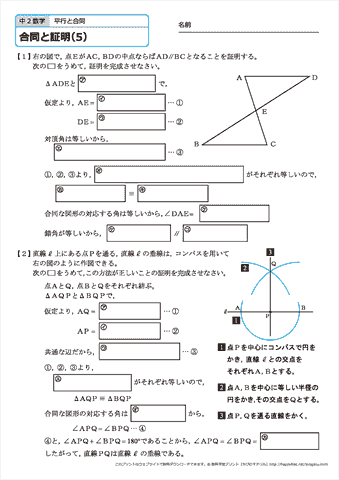



中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
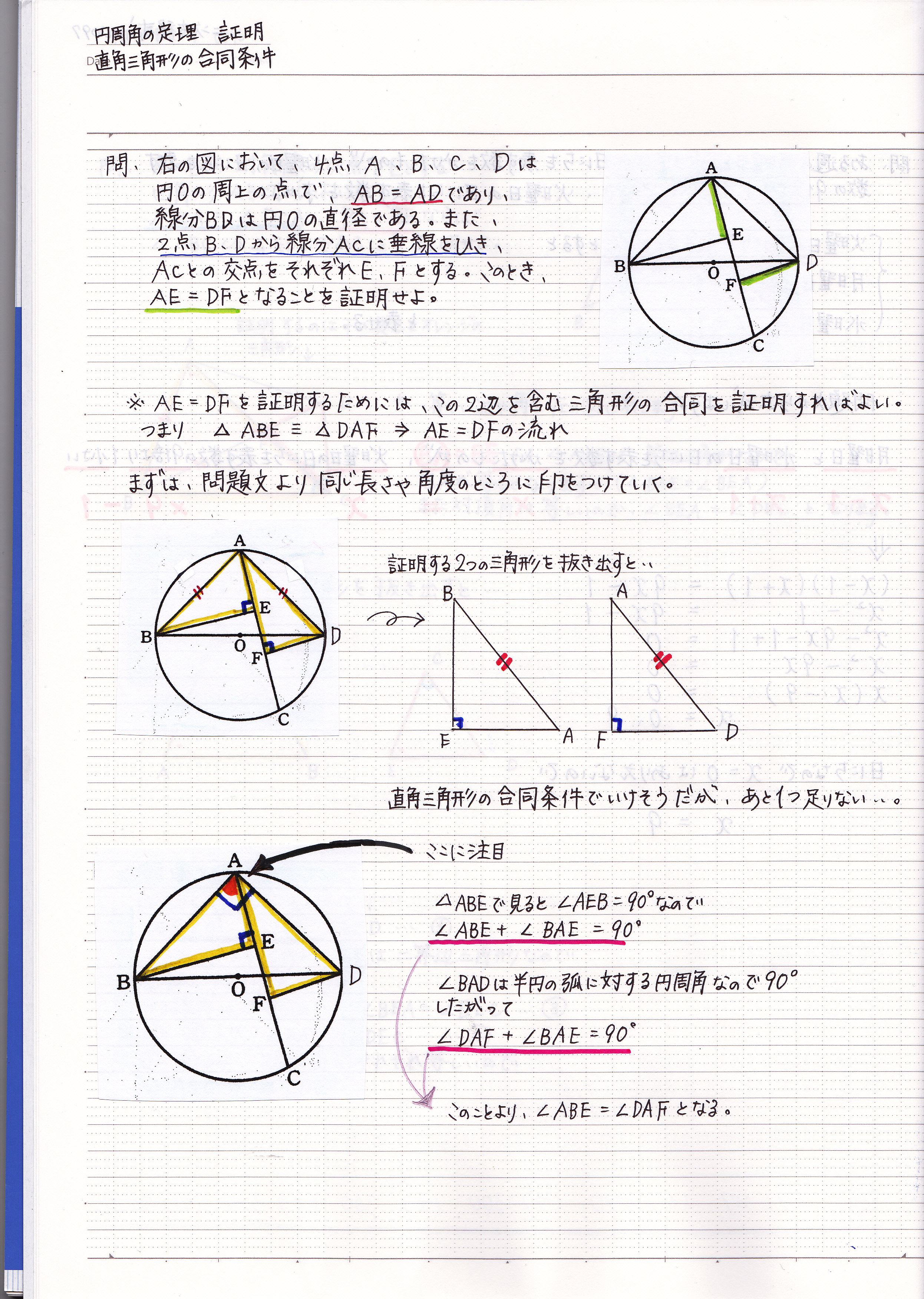



直角三角形の合同条件を使った証明問題の解き方 現役塾講師のわかりやすい中学数学の解き方




中2 証明 暗記集 中学生 数学のノート Clear
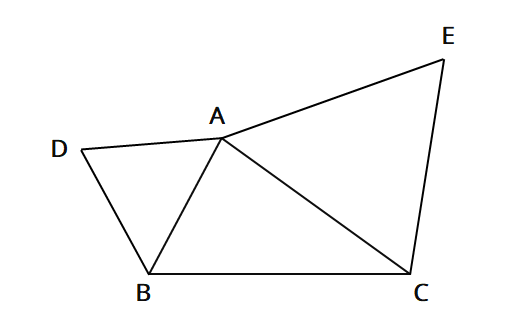



中2数学 三角形の合同の証明応用問題 中学生勉強サイトあかね先生
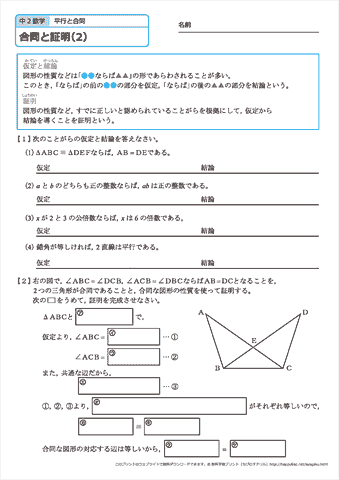



中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




世界一わかりやすい数学問題集中2 5章 図形の性質と証明
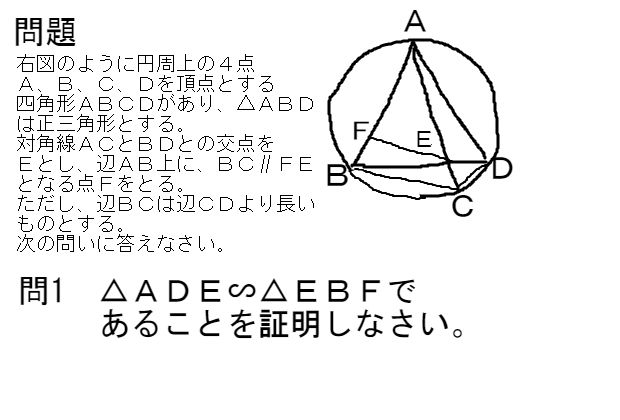



超難問入試 円と三角形 証明と求積問題 中学数学 理科 寺子屋塾の復習サイト




心に強く訴える数学 図形 証明 最高のぬりえ




図形の折り返しと三角形の相似の証明 解き方 現役塾講師のわかりやすい中学数学の解き方




世界一わかりやすい数学問題集中2 4章 平行と合同と証明




無料 中3数学 標準問題 解答プリント 327 図形の相似2 相似条件と証明



Studydoctor図形の性質と相似の証明 中3数学 Studydoctor




中学3年の数学 動画 相似の証明チャレンジ lv 1の問題 19ch




中3数学 式の計算の利用 数に関する証明 まとめと問題




メルカリ 中古理由あり 中学数学図形の証明がらくらく解ける 参考書 400 中古や未使用のフリマ
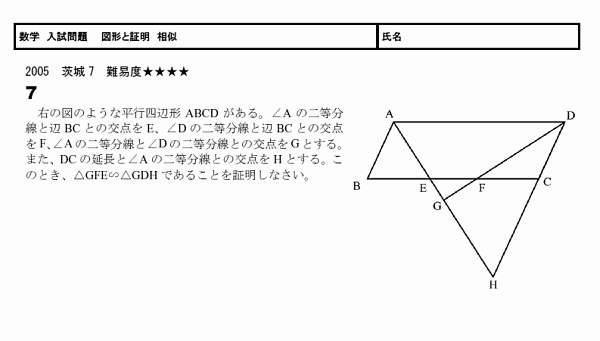



図形と証明 相似 無料学習プリント教材




21年版 中学生におすすめの 数学 問題集ランキング




直角三角形の合同条件とその証明 数学fun
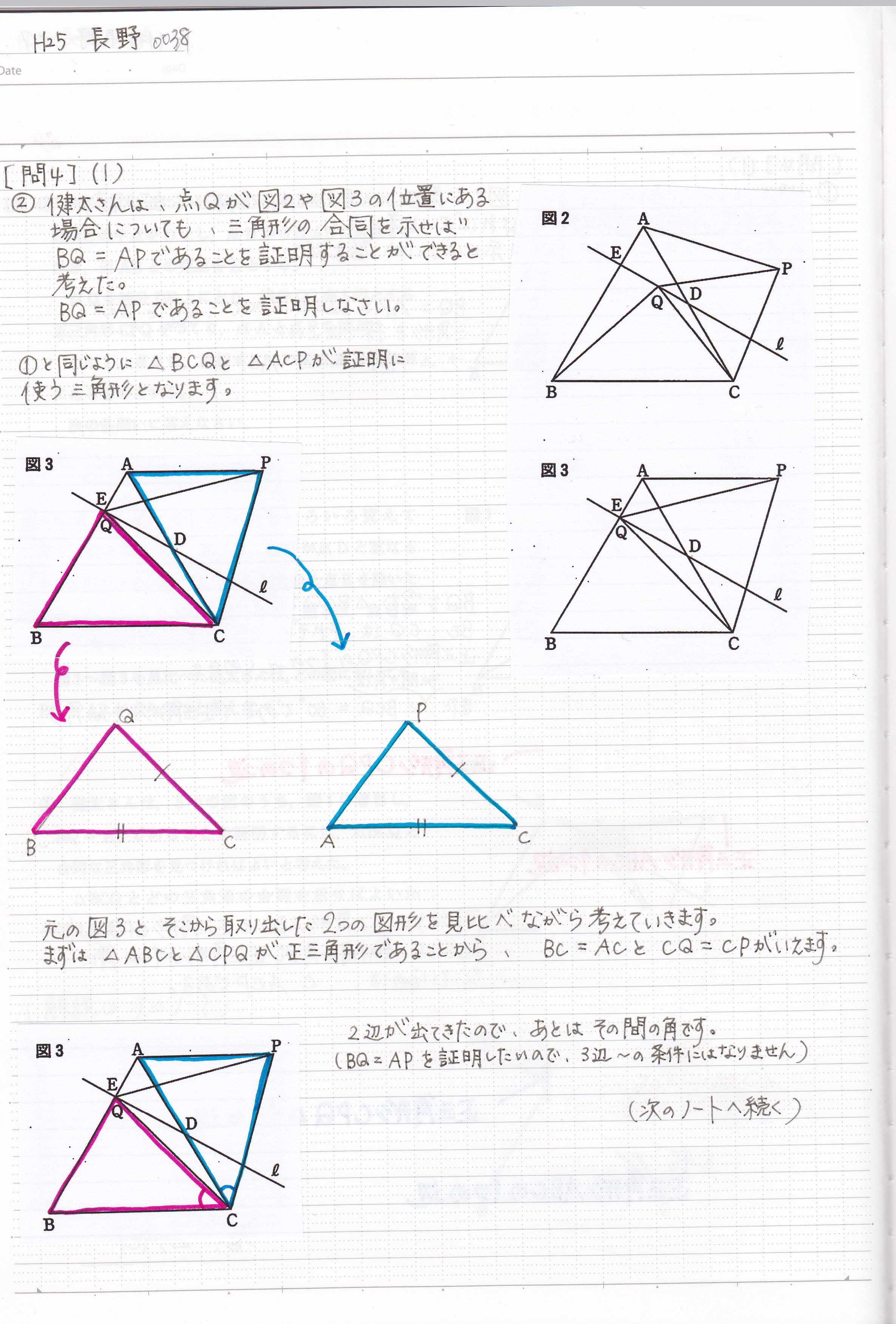



平成25年長野県立高校 入試問題 図形の証明問題 合同 現役塾講師のわかりやすい中学数学の解き方
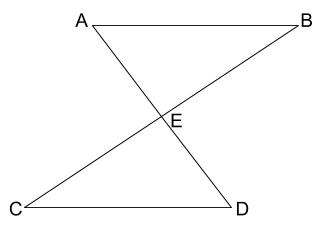



中学数学 三角形の合同の証明 その1 中学数学の無料オンライン学習サイトchu Su



中3数学12 図形の相似2 相似条件と証明 基本解説プリント 問題 327
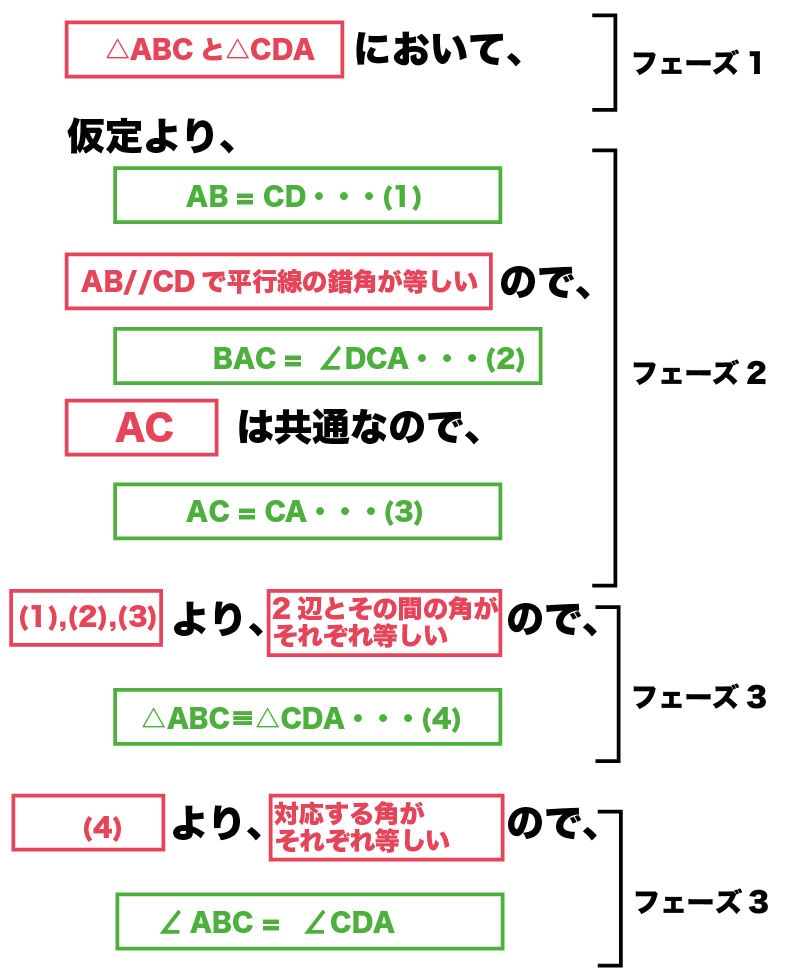



中学数学 3年間つかえる証明問題の書き方 Qikeru 学びを楽しくわかりやすく




中学3年 数学 東京書籍 新しい数学 相似な図形 平行線と比 赤城 ᐡᐤᐡ



U9j580gf8iba369ji2w Xyz P 608



1




数学 中学証明問題を解く4つのポイント




数学 中3 59 円周角の証明チャレンジ Lv 1 Youtube



4gr7x76yz2id1fo99eleb Com Benkyou Suugaku Syoumei Html




中学2年 数学 証明まとめ 中学生 数学のノート Clear
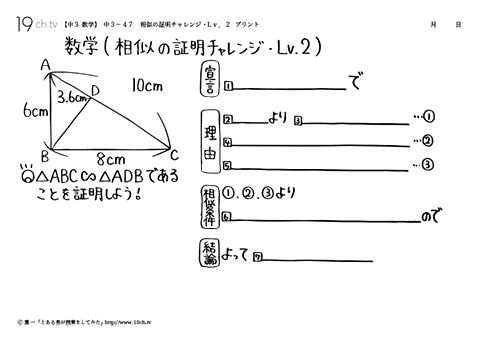



中学3年の数学 動画 相似の証明チャレンジ lv 2の問題 19ch
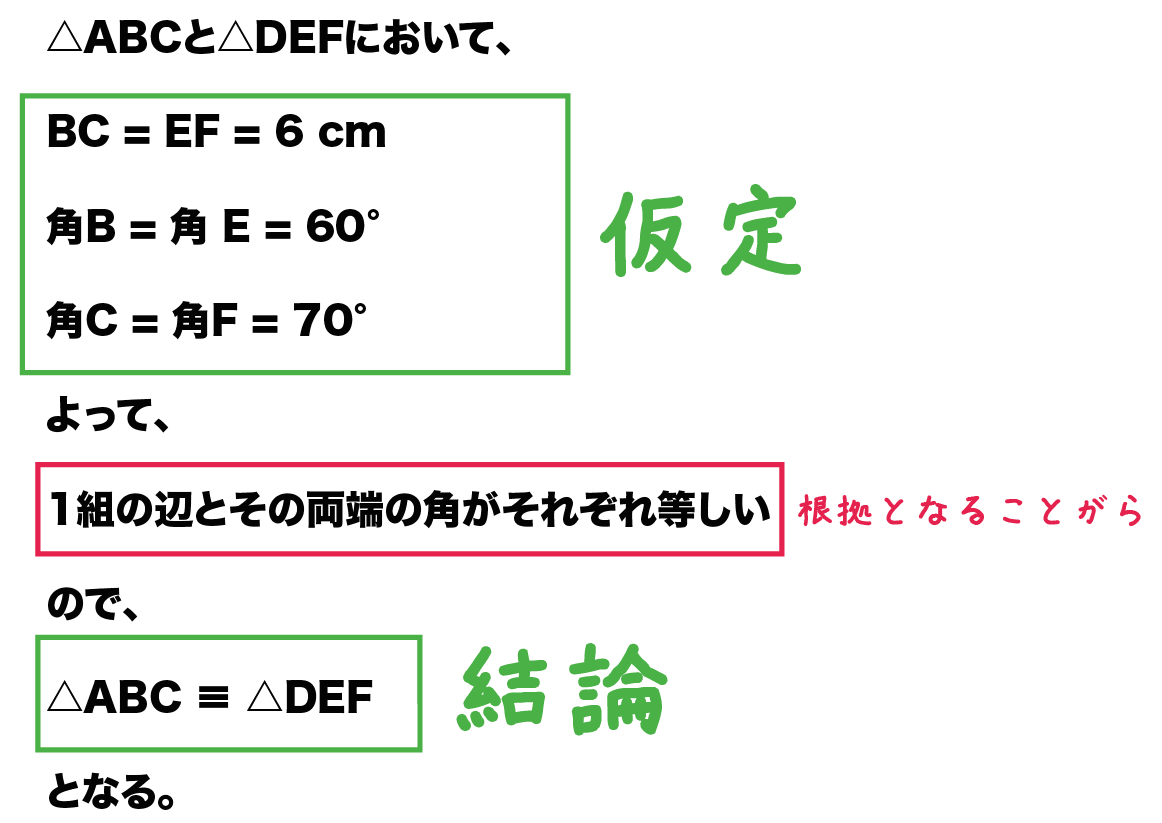



中2数学 証明とはいったいなにもの Qikeru 学びを楽しくわかりやすく




中学校 平成24年度教科書 数学 チャート式の数研出版




中学数学 図形の証明がらくらく解ける 中学数学らくらく解ける シリーズ 学研教育出版 本 通販 Amazon
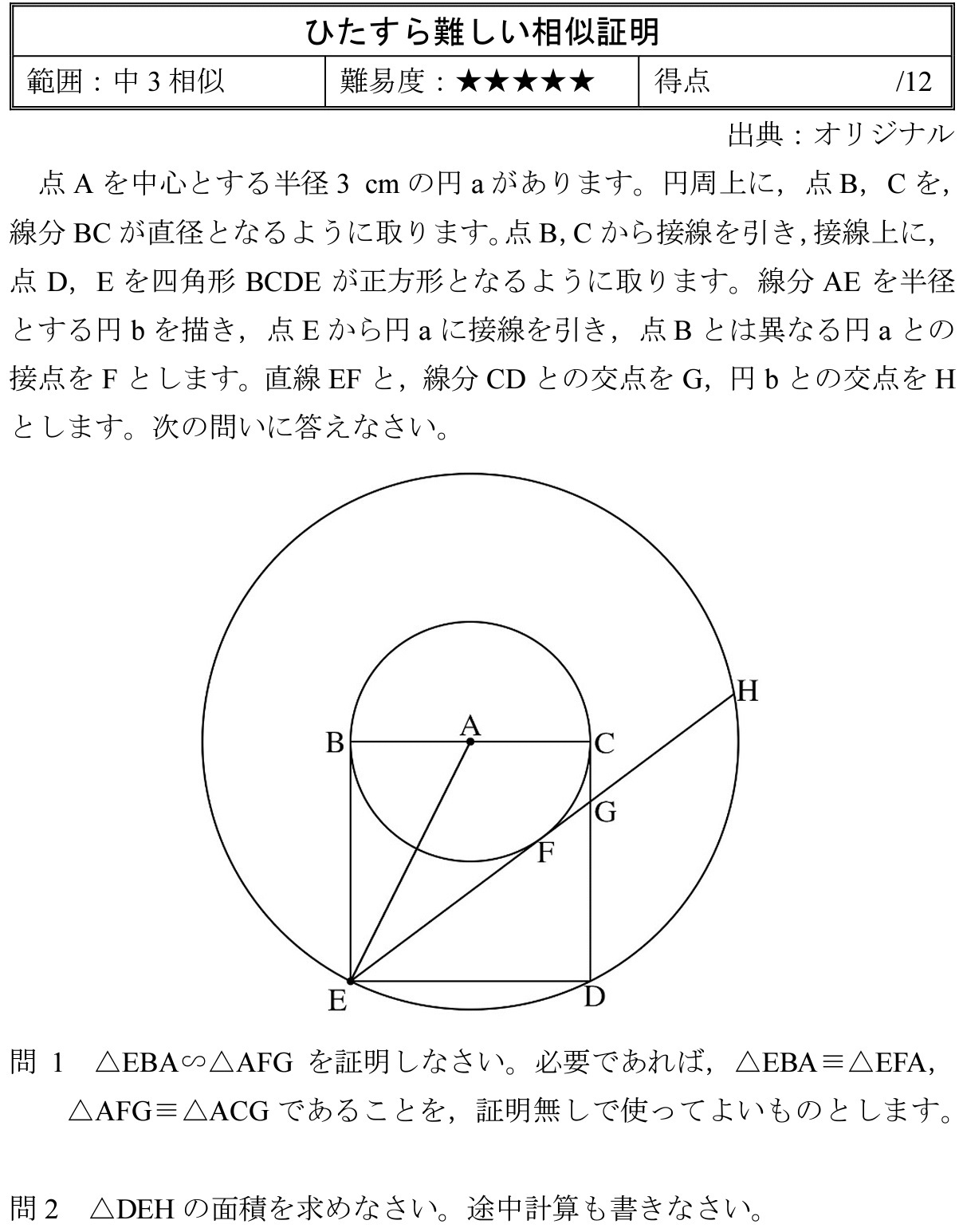



ひたすら難しい相似証明 オリジナル 高校入試 数学 良問 難問




中2数学 証明とは 例題編 映像授業のtry It トライイット



Q Tbn And9gcs8jzs Zkdiyrmuisoi0mwqzez E9r9gwygbti5ixce9rlyfs0 Usqp Cau




中学数学3 平行線と線分の比の証明 中学数学 By となりがトトロ マナペディア




中3数学 円の性質と証明 練習編 映像授業のtry It トライイット




中学数学 証明は簡単 合同な図形を探すたった1つのポイント 烈志塾 塾長ブログ




中学数学が秒でわかる 正三角形の中に正三角形がある図形の証明 超 解説付き なぜか分かる はかせちゃんの怪しい研究室
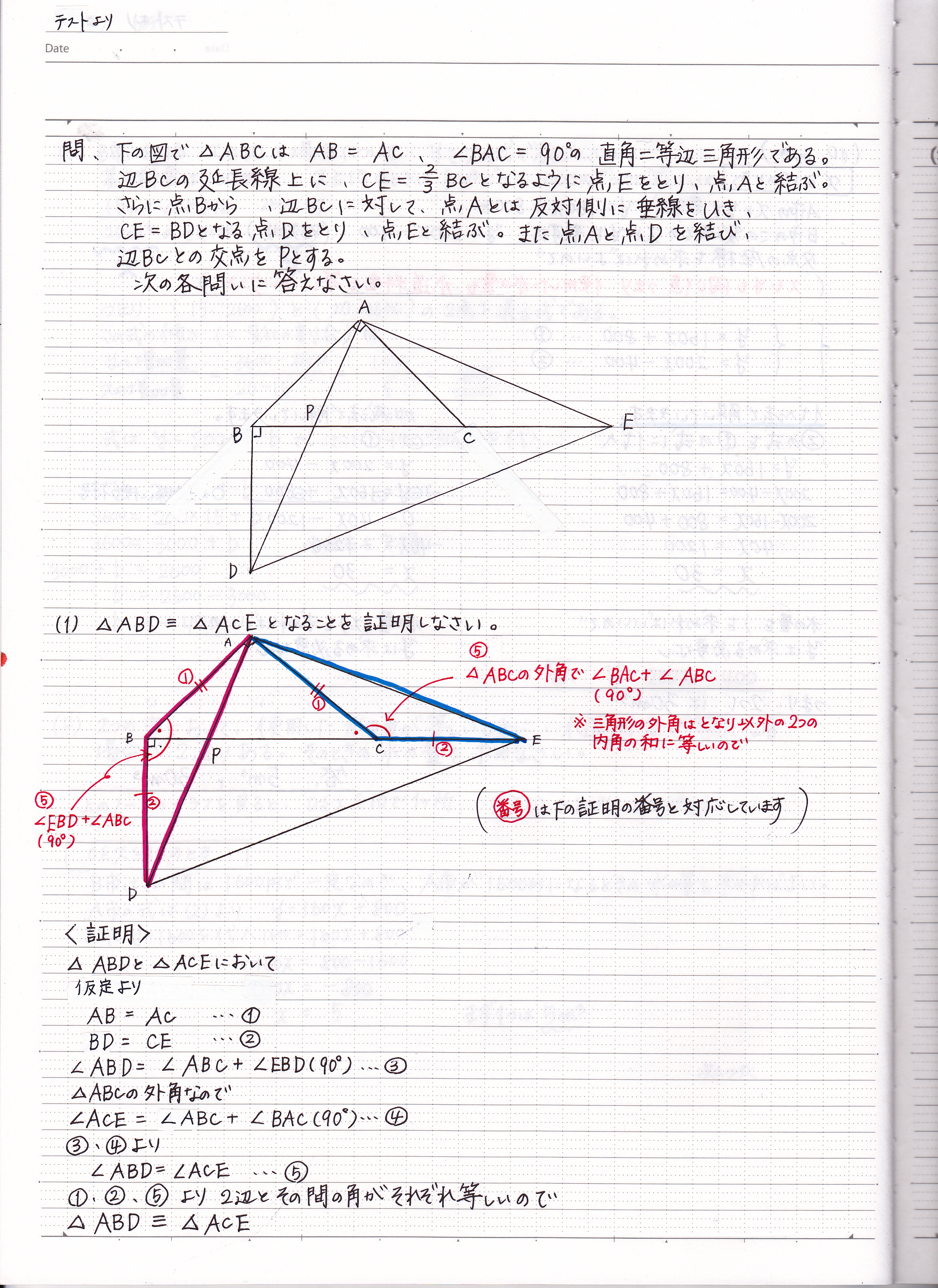



図形の総合問題の解き方 合同証明 三平方の定理 相似など 現役塾講師のわかりやすい中学数学の解き方




中3数学 円の性質17 円の性質を利用した証明 すべて無料 星組の中学数学講座



中3第1章23式の計算の利用 整数の性質の証明 中学数学 1学期




中3数学 整数問題の証明2 連続する数 例題編 映像授業のtry It トライイット
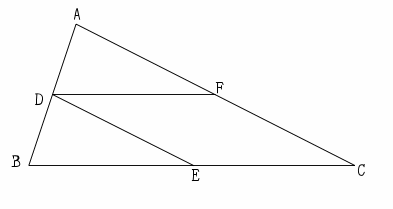



合同の証明2




数学 中2 60 証明のしくみ Youtube




3年ー5章ー図形と相似 ワカデキな中学校数学
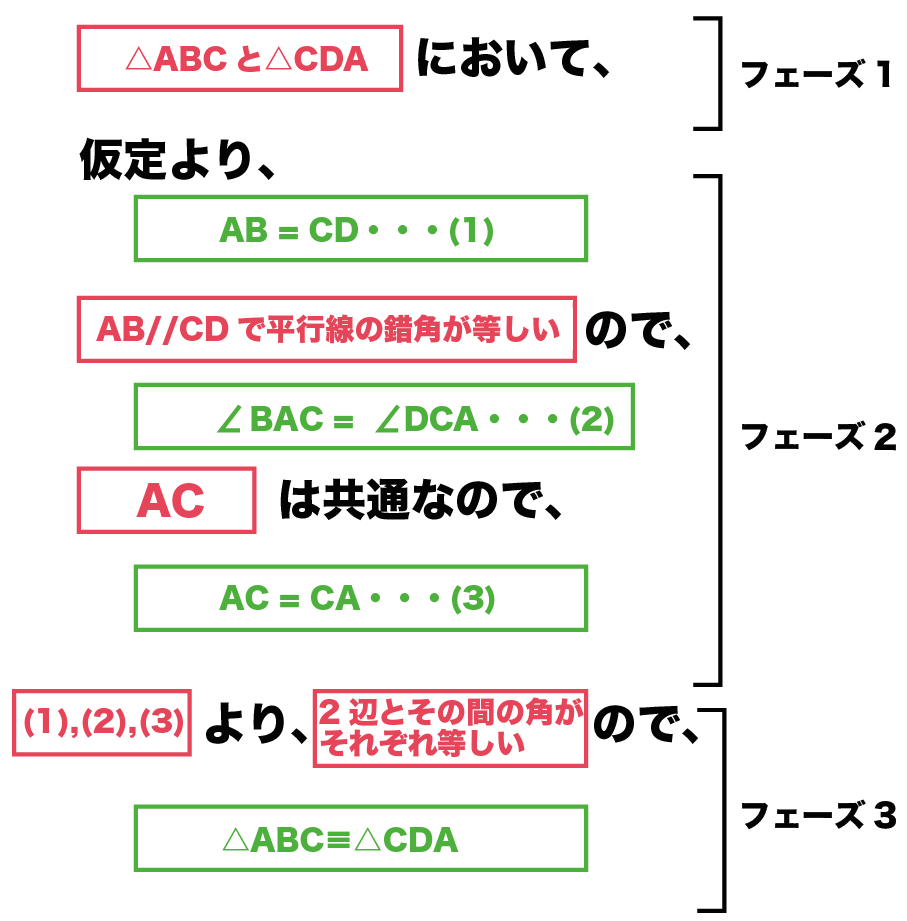



中学数学 3年間つかえる証明問題の書き方 Qikeru 学びを楽しくわかりやすく



中3数学 相似の証明のポイントと練習問題




最高中 3 数学 証明 最高のぬりえ
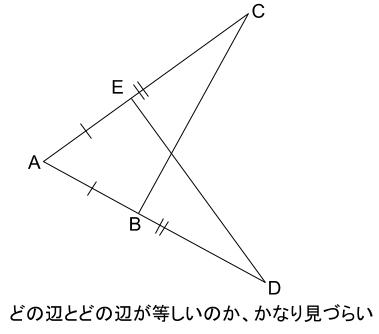



中学数学 三角形の合同の証明 その2 中学数学の無料オンライン学習サイトchu Su



中2数学 直角三角形の合同条件と証明問題 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト
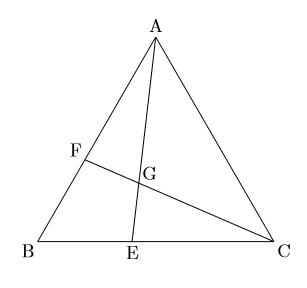



中学数学 攻略 三角形の合同 数樂管理人のブログ




無料 中2数学 基本解説 問題プリント 226 図形6 証明のしくみと根拠
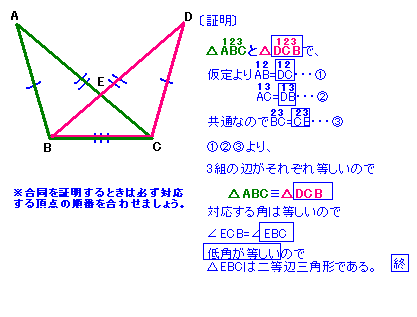



中学数学の問題を解くコツ




中3数学 相似の証明問題 練習編 映像授業のtry It トライイット




最高中学 数学 証明 やり方 最高のぬりえ




中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
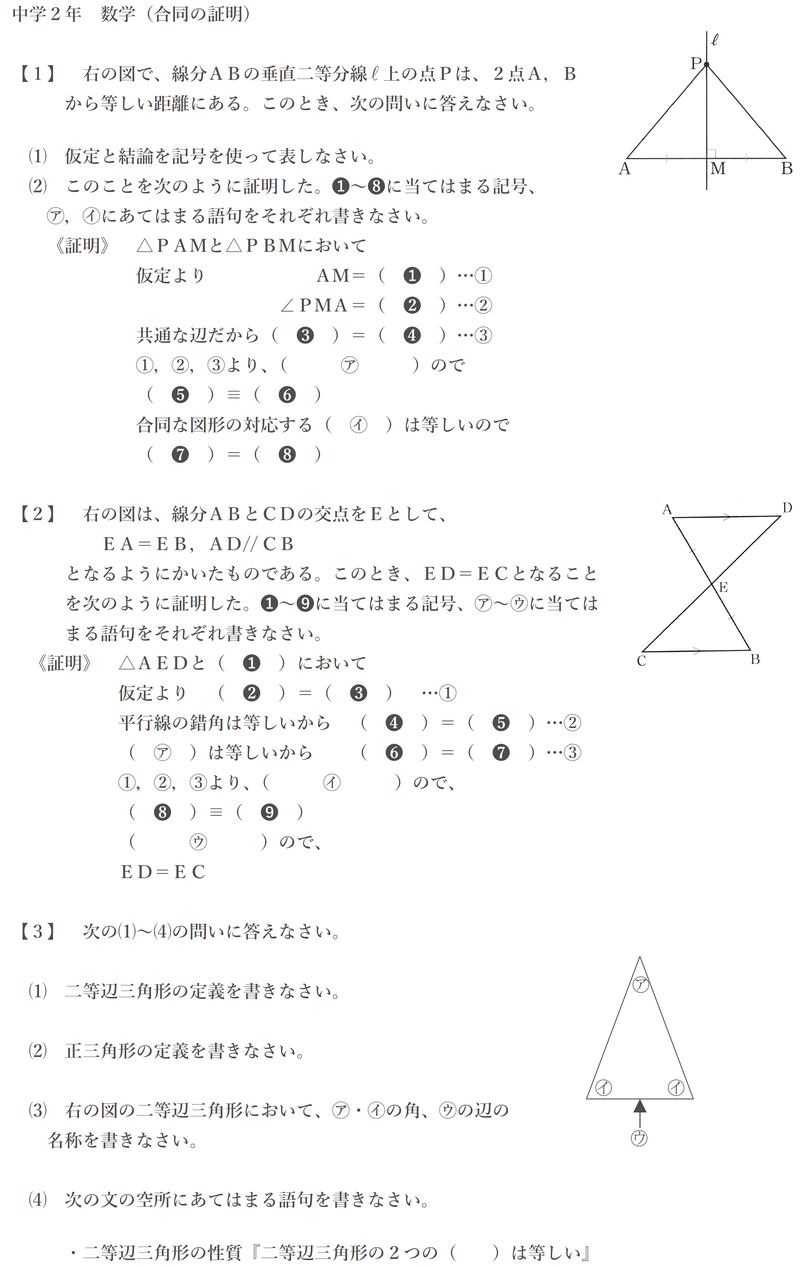



中2数学 三角形の合同の証明の流れ 3学期期末テスト用 赤城 ᐡᐤᐡ
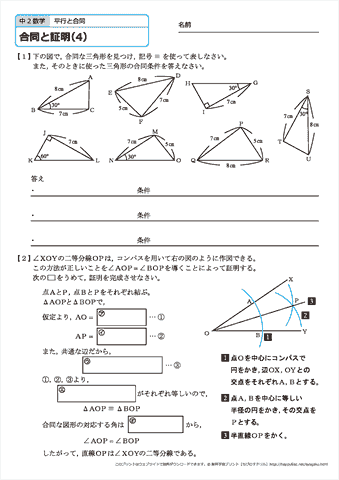



中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




数学 中3 14 式の計算の利用 図の証明編 Youtube




中2 証明 中二 中学生 数学のノート Clear
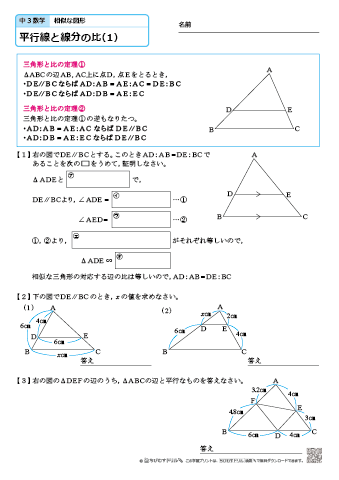



中学3年生 数学 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




平行四辺形の証明問題 無料で使える中学学習プリント
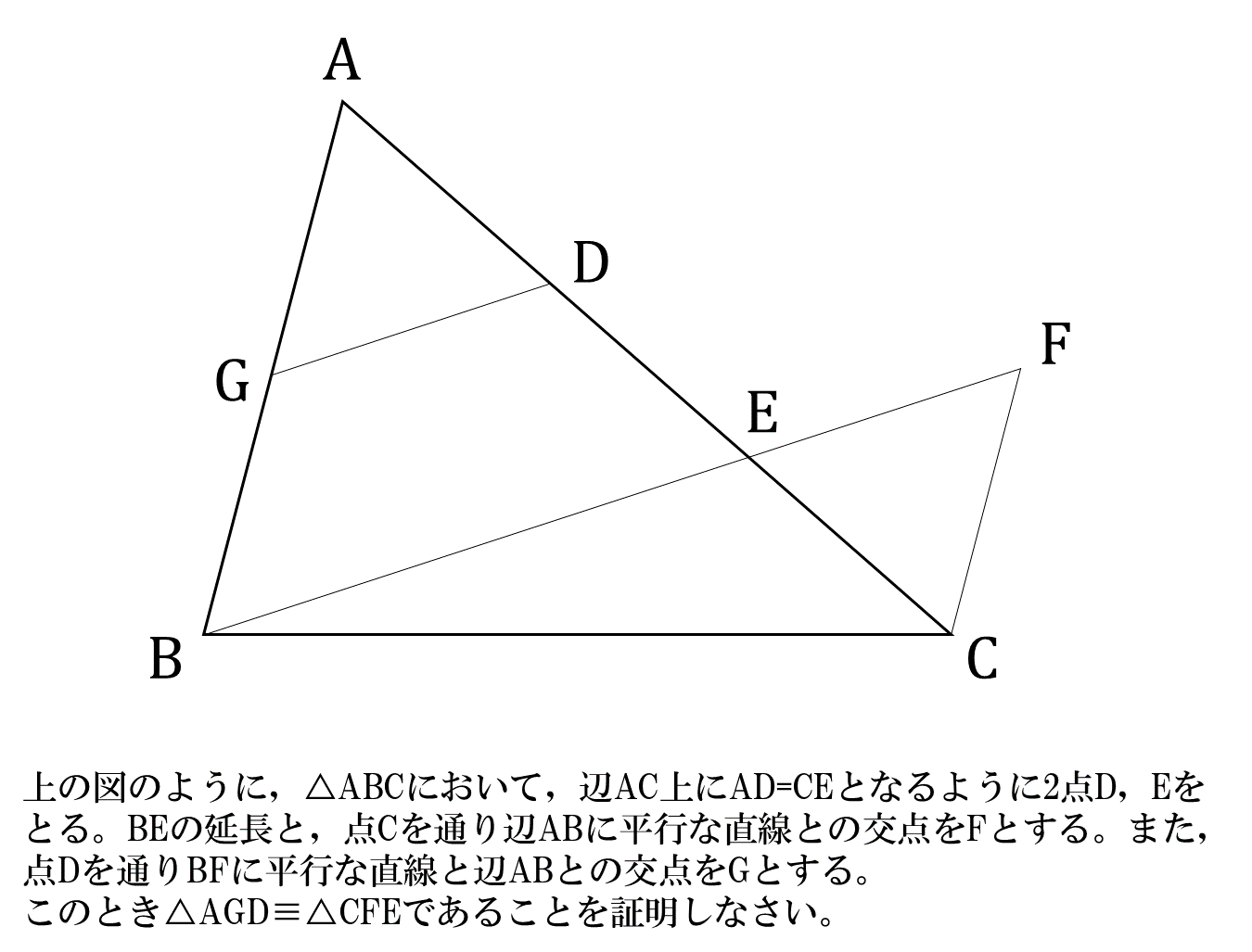



数学 中学証明問題を解く4つのポイント



三角形の相似条件 ドリるーむ



0 件のコメント:
コメントを投稿