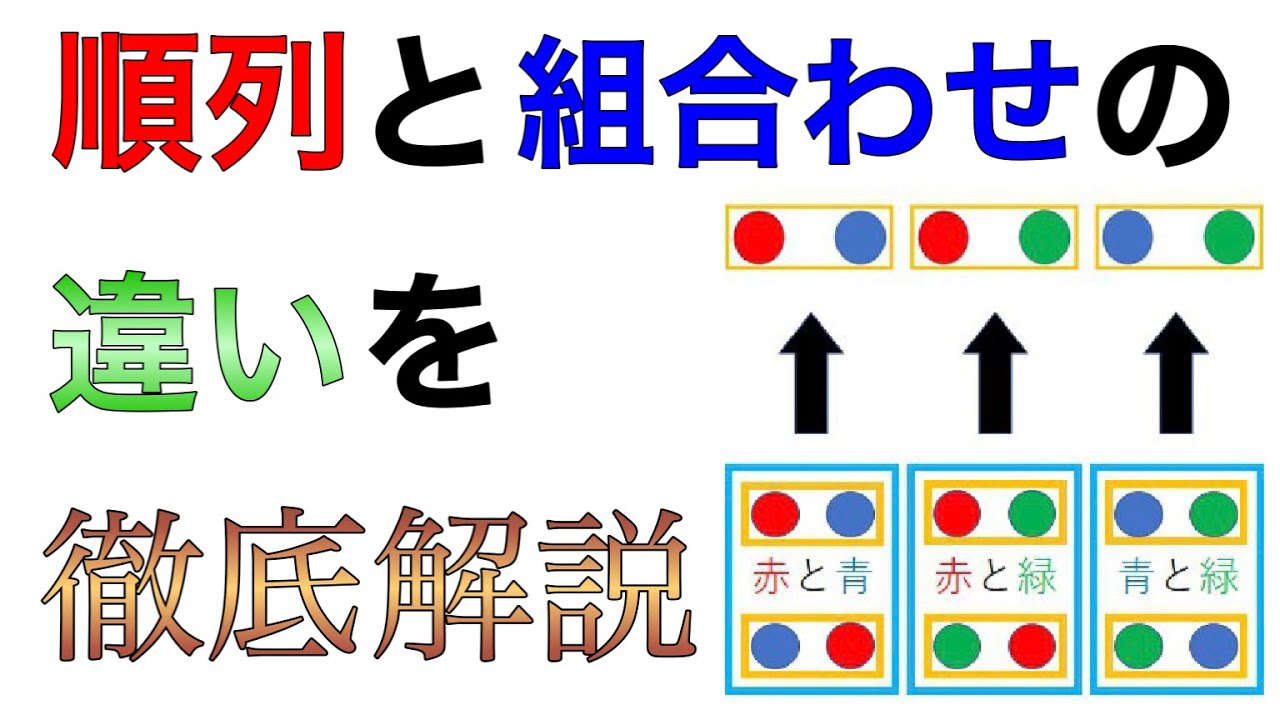
①は順列で、答えは 5 P 2 =5×4=通り ②は組み合わせで、答えは 5 C 2 =5×4÷2=10通りになります。 今回は、そんな順列と組み合わせの数の考え方についてです。 photo creditWilliam Warby順列・組合せの問題に挑戦! 順列・組合せの問題は、確率論、計算数学、オートマトンの理論および数理経済学において きわめて重要である。しかし、現行の教育課程においては、深く考えさせる問題が少なく、十 分な訓練ができる状況にはない。ここで JavaScriptで"順列"と"組み合わせ"の説明ですがとてもわかりやすいです。 再帰処理で求める順列(nPr)JavaScript Qiita この記事について プログラミングクイズを解くにあたり、再帰処理を使うとスラッと解けそうな気がする問題がいくつかありま qiitacom 順列とは 異なる n 個のものの中から r 個

場合の数 は 順列 の計算の応用 中学受験プロ講師ブログ
順列 と 組み合わせ
順列 と 組み合わせ- 順列と組み合わせの違いは、選び出した/取り出したものの 並び順を考慮するかどうか です。 「順列」は取り出したものの 並び順を考慮 しますが、「組み合わせ」では 並び順を考慮しま 同じものを含む順列 例 a5個、b3個、c2個の合計10個の文字をすべて1列に並べる順列の総数 考え方1同じ文字の位置を選ぶ 先頭から最後尾まで10個の場所からaを置く位置を5つ選ぶ 10 C 5 のこりの場所からbを置く位置を3つ選ぶ 5 C 3 のこりの場所からcを




場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん
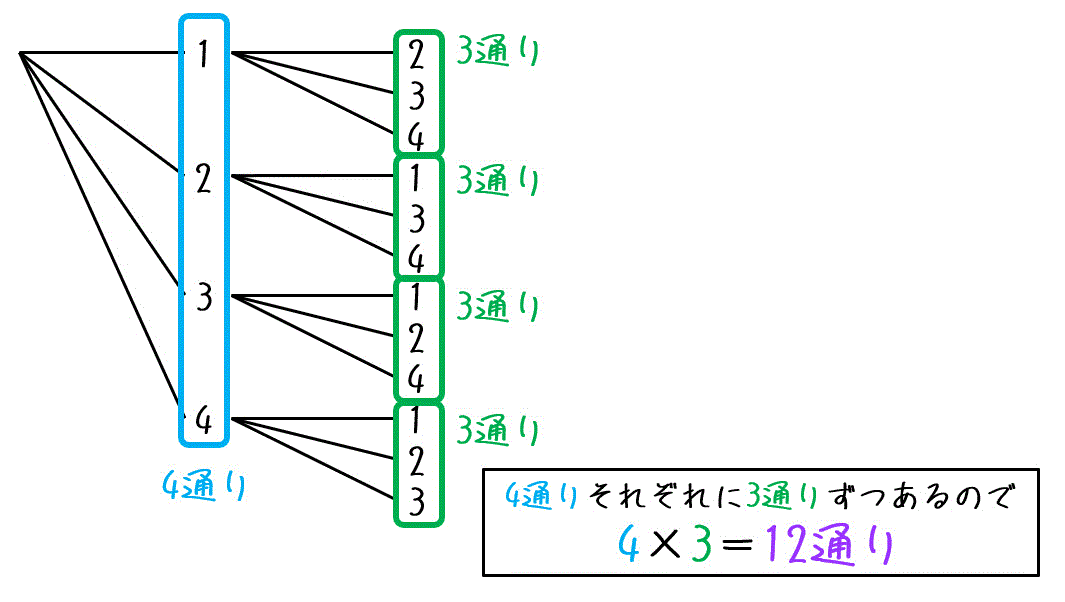
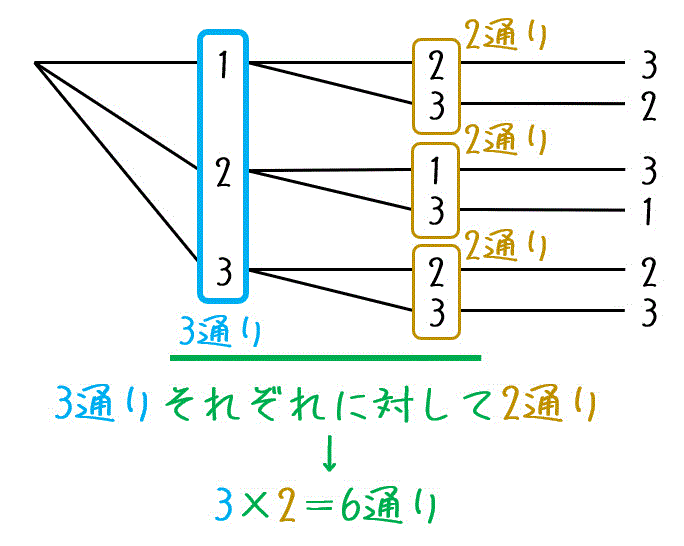
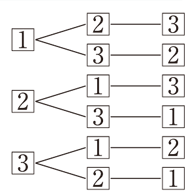
組合せとは いくつかのものからいくつかのものを取り出して 並べる ことを 順列 と呼んでいました.ここでは,取り出したときの順序を考えない場合の数を考えてみましょう.そのような問題は 組合せ の問題と呼ばれています. 順列 → → 順序を考慮つまり、 順列では、並べる順序を問題にして考えますが、組合せでは順序を 問題にしないで取り出し方だけを問題 にして考えます。 したがって、順序が問題になる取り出し方の場合は順列で、順序が問題に ならない取り出し方の場合は組合せで考えればいいわけです。 では、問題を考えてみましょう。 1 (1)は「第1走者から第4走者までの4人を選ぶ順列、組み合わせ、円、重複、組分け。これらの場合の数の違いとその見分け方を簡単に解説します。 ここでは共通の例として、7個のガラス玉があった場合を考えてみます。 順列 7個のガラス玉から3個選んで一列に並べる $_7p_3$ 組み合わせ
= 7 ・ 6 ・ 5 ・ 4 ・ 3 ・ 2 ・ 1 = 5040 7 P 7 = 7!順序を区別すれば,項の数は「重複順列」 2 3 =8 通りになる =a 3 3a 2 b3ab 2 b 3 文字の部分が同じものを同類項として整理すれば,文字の組合わせは a 3 , a 2 b , ab 2 ,b 3 で 2 H 3 =4 種類になる ※ これらのうち,順列と組合せには, n P r =r!異なる n個のものから 重複を許して r個を選ぶ組み合わせの総数を求めます。 重複組合せ(表) 異なる n個のものから、重複を許して r個を選ぶ組み合わせの総数の rを変化させた表を求めます。 順列 異なる n個のものから r個を選んで並べる順列の総数 nPr を求めます。 順列(表) 異なる n個のものから r個を選んで並べる順列の総数 nPr の rを変化させた表を求め
みんなで数学 ~楽しく学ぶ『順列・組合せ』~ 市立札幌大通高等学校 清水 貞人 (数学教育協議会会員) 『連結ロケット』は百円ショップで購入できる7色の連結式クレヨンです。以下は高校での授業例で すが、レクレーションなど授業以外の場面でも子どもからお年寄りまで年齢に関係なくN C r の関係があるが順列と組み合わせ 一般に,互いに異なるn個のものからr個取り出して,それを1列に並べるとき,その並べ方を,n個のものからr個取る順列といいます。 上の例は,3つの違った数1,2,3の順列をつくる問題ですが,これを右のような図に,順序よくかいていくと,すべての場合を落ちなく重なりなくあげることができ,順列の数6も求められます。 このような図を樹形




数1a 順列 組合せ 21 重複組合せ と を並べるやつ Youtube
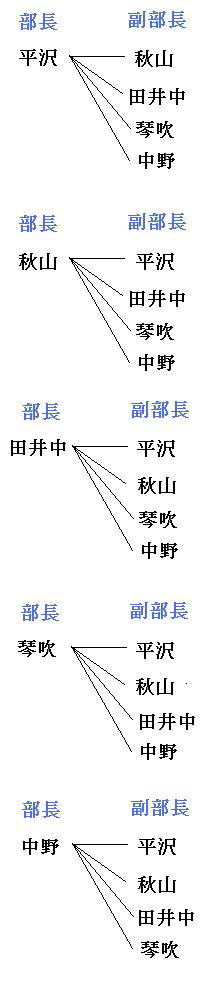



組合せと順列は何が違うのか 組合せは樹形図でも計算でも解ける
今回の記事では、順列・組み合わせを求める際に使用します。 itertoolsのインストール方法 itertoolsはPythonの標準ライブラリなのでインストールの必要はありません。 順列 順列とは、異なるn個の中から k 個を順番をつけて並べる場合の並べ方です。 総数は n P k で表され、以下の公式順列と組合せ 順列とは,互いに区別で きるものを1列に並べる ときの並べ方の数,組合 せは,互いに区別できる ものから何個か取り出す ときの取り出し方の数を 言う.組み合わせは、順序に意味がある順列とは異なります。 総数 = n、抜き取り数 = r とすると、組み合わせの総数は、次の数式で表されます。 問題3それぞれA,B,Cと書かれたカードがあります。



Excelを使った数値計算ツールsuitexl



順列組合せの公式はp 総乗 を使うべき 万象酔歩
順列・組み合わせ 辞書順列・組合せの問題の見分け方 このページでは、順列・組合せの問題を見たときに、 どのポイントを押さえれば解き方を見分けることができるのかについて解説します。 まず、「順列」か「組合せ」かを見分ける。 初めに、その問題が順列なのか、組合せなの�順列と組み合わせ ここでは、順列と組み合わせの違いについて、できるだけわかりやすく説明していきます。 で計算をする順列と、 で計算をする組み合わせ。 この使い分けに迷っている人も多いでしょう。具体的にそれぞれの計算式が使われる数学・算数 順列・組み合わせ いつもお世話になっております。 高校1年生の者です。 テスト前のためずっと勉強をしているのですが、 数学の順列・組み合わせでわからない問題があります。 問 3人乗 質問No



重複順列 Itパスポート出題テーマ別過去問題 平成24年度秋期 テクノロジ系 問78




順列と組み合わせの公式とその違い 問題付き 理系ラボ
定義:順列 permutation この文脈で、 n C r は「n個のものからr個とった組み合わせ 」と呼ばれる。 ・ n P r は、r個の同一要素を異なった順序に並べかえたものを、( たとえば、{a,b,c}{a,c,b}{b,a,c}{b,c,a}{c,a,b}{c,b,a} )別のものとしてカウントしている。 これらをまとめて一つとしてカウントするよう頑張って解いてみてください。 解答 (1) 7 P 7 = 7!= 7 ・ 6 ・ 5 ・ 4 ・ 3 ・ 2 ・ 1 = 5040 通り。 (2) まず、男子 2 2 人を両端に並べてから、残り 5 5 人の並べ方を数えればOK。 ⅰ)男子 4 4 人から 2 2 人を両端に並べる 4 P 2 = 4 ・ 3 = 12 4 P 2 = 4 ・ 3 = 12 通り。 ⅱ)残り 5 5 人を並べる 5!



数列 順列 組み合わせ計算機 On The App Store




順列と組み合わせの公式とその違い 問題付き 理系ラボ
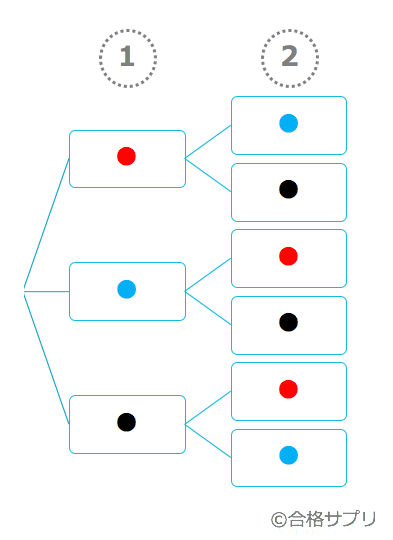
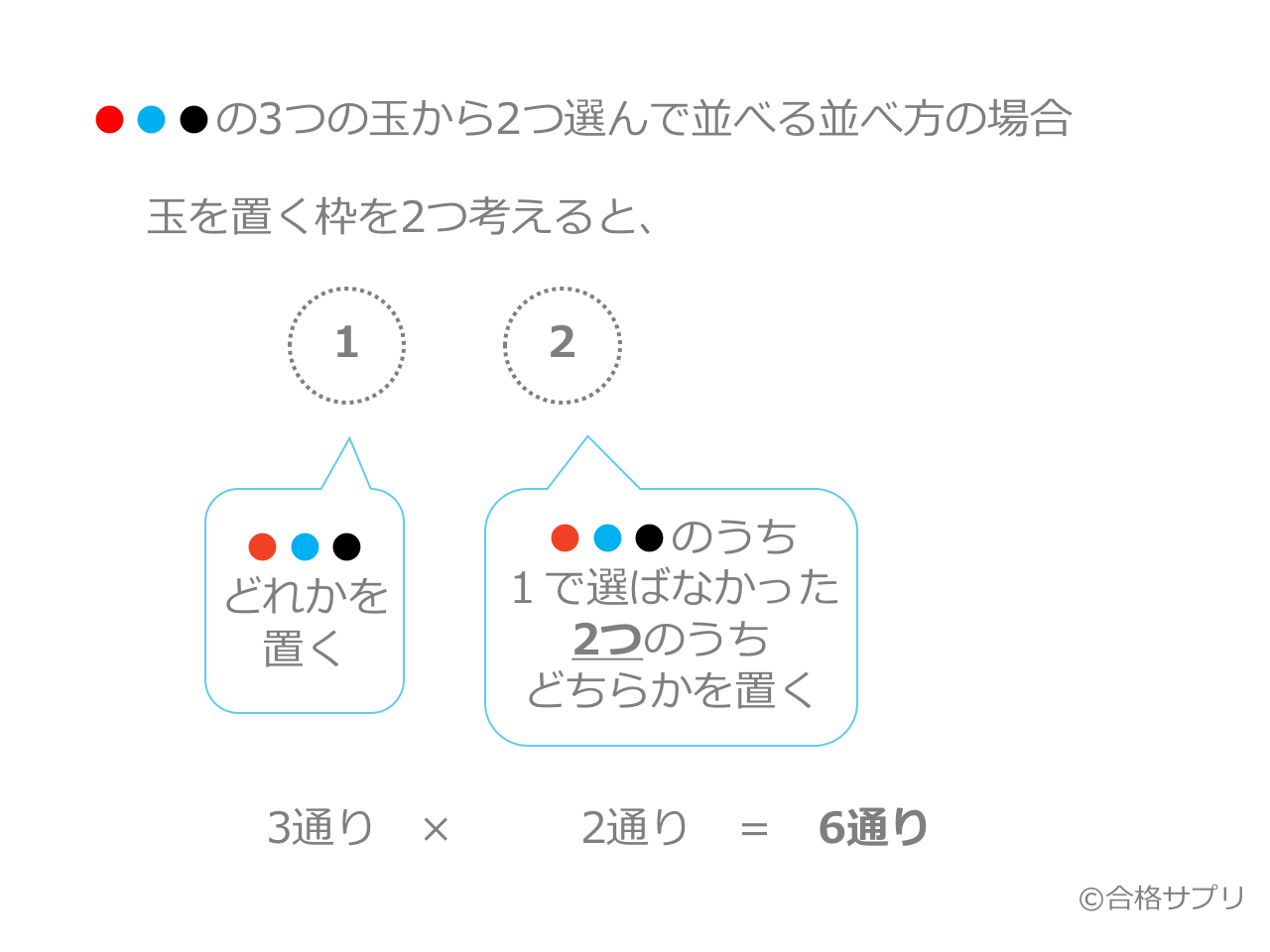
= 5 ・ 4 順列と組合せの違いは以下です: 順列 :「選んで並べる」「ABとBA を区別してそれぞれ数える」 組合せ :「選ぶだけで並べない」「ABとBAは区別せず同じもの」研究主題「数学的活動を生かした同じものを含む順列の指導」 実践研究員 濱辺 望(新潟県立津南高等学校教諭) 要約 数学A「順列と組合せ」の中の「同じものを含む順列」を題材にした。この内容では、ただ単に 「公式を教える 「やり方を教」、 える」という形式的な授業になりがちである




場合の数 は 順列 の計算の応用 中学受験プロ講師ブログ




高校数学a Npr と Ncr の使い分け 練習編 映像授業のtry It トライイット
= 5 ・ 4 ・ 3 ・ 2 ・ 1 = 1 5!前回 https//wwwyoutubecom/watch?v=gkeQK_kfa5w 次回 https//wwwyoutubecom/watch?v=4LJtn7VG67Mサブチャンネル とある男がゲームを日本大百科全書(ニッポニカ) 順列・組合せの用語解説 n個の異なるものからr個を取り出して1列に並べたものをn個からr個とる順列といい、その総数をnPrと書く(Pは、順列の英語permutationの頭文字をとったもの)。たとえば、4個の文字A、B、C、Dから3個をとって並べると、次のような24通り
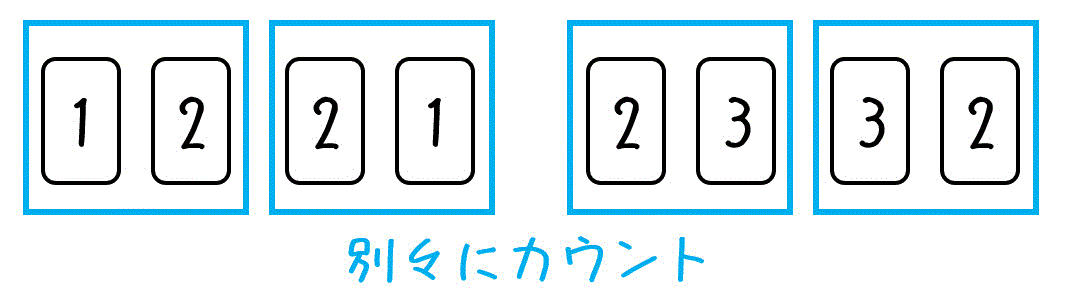



うさぎでもわかる場合の数 順列と組み合わせの違い 工業大学生ももやまのうさぎ塾



うさぎでもわかる場合の数 順列と組み合わせの違い 工業大学生ももやまのうさぎ塾
SPI 場合の数 順列・組み合わせの基礎 この単元の基礎は分量が多いです。 頑張って学習しましょう! ! 1 PとCの使い分けの解説です。 <問題> 1~3のカードが1枚ずつある ① 2けたの整数は何通りできるか ② 2枚選ぶのは何通りあるか 順列の全組み合わせを作成するFunction 配列を与えると、 再帰処理で順列の全組み合わせを作成 します。 結果は、 2次元配列で返します。 Public Sub permutation (ByRef aryIn, ByRef aryOut, Optional ByVal i As Long = 0) Dim j As Long Dim ix As Long Dim sTemp Dim ary If i < UBound (aryIn) Then高校数学で勉強する順列(Permutation)、組合せ(Combination)、重複組合せ(Homogeneous product)を求めるプログラムを作成します。 <順列の公式> <組合せの公式> <重複組合せの公式> 公式だけではわかりにくいので例題を以下に示します。 例題 ここはある中学校です。あるクラ




数列 順列 組み合わせ計算機 On The App Store




Permutation And Combination 順列と組み合わせ Math In English 13 Okenavi
順列と組み合わせ の部分一致の例文一覧と使い方 該当件数 10 件 例文 順列と組み合わせ 例文帳に追加 permutation (s) and combination (s) 研究社 新英和中辞典 順列と組み合わせ の取得方法 例文帳に追加 METHOD OF ACQUIRING PERMUTATION AND COMBINATION 特許庁 数学に順列 順列(表) 順列(重複あり) 順列・重複あり(表) 円順列 円順列(表) 数珠順列(じゅず順列) 数珠順列・じゅず順列(表) 順列や組み合わせなどを わかりやすくまとめてみて これまでの生活ではなかなか出番がなかったのですが、 いざやってみると計算自体はかけ算なので難しくはなく、 普段の生活でも取り入れていきたいなと思えるようになりました。 アオキ ちょくちょく見返しつつ実生活でも使うように



うさぎでもわかる場合の数 順列と組み合わせの違い 工業大学生ももやまのうさぎ塾




重複順列の問題6選とは 公式よりも応用問題の解き方が大切です 遊ぶ数学
順列と組み合わせでどっち使ったらいいのか分からない人が多くいらっやると思いますが、 これは、見分けるのがめちゃくちゃ楽です。 順列は、場所が決まってる、組み合わせは決まってないって教わるかもしれないけど、 これは何が言いたいのか正直分からん。 なので、ド文系君風にA11 順列、組み合わせ、重複組合わせ 本節では 重複順列以外に高校数学でも馴染みの深い「順列」、「組み合わせ」、「重複組み合わせ」といった概念を Mathematica を用いて吟味する。 1 順列 まずオブジェクト、 "bn,k"、を構築する。これは、「異なるn個のものから重複を許さずk個を




場合の数 重複組合せ と 重複順列 の違いをわかりやすく解説します




1 順列と組み合わせについて 数学帝國への逆襲 西春自習質問教室のブログ




場合の数 順列 組合せ のブログ記事一覧 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください




順列と組合せの違いってなんでしょうか 調べてもあまりよくわからないです Clear




なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ




順列と組み合わせの公式とその違い 問題付き 理系ラボ




3分で分かる 順列と組み合わせの違いと公式をわかりやすく 練習問題つき 合格サプリ



順列と組み合わせの違いと見分け方 公式や計算問題 受験辞典



うさぎでもわかる場合の数 順列と組み合わせの違い 工業大学生ももやまのうさぎ塾




機械学習の統計学 順列と組み合わせって何 ししまる みらいのクルマをつくる人 Note




重複順列と重複を許して取る組み合わせの違い がよく分かりません お願いします Clear



組み合わせ C とは 公式や計算方法 は何通り 受験辞典




場合の数 順列 P と組合せ C の違いは どう使い分ける ますますmathが好きになる 魔法の数学ノート



1
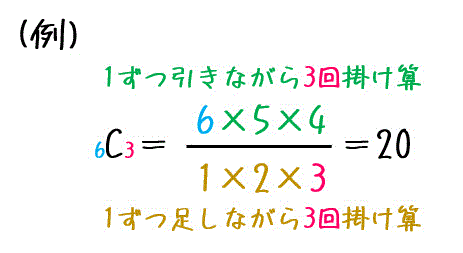



うさぎでもわかる場合の数 順列と組み合わせの違い 工業大学生ももやまのうさぎ塾




数学 P と C の 違い 確率の問題で コンビネーション C とパーミテーション P の違いを教えてください Amp Petmd Com



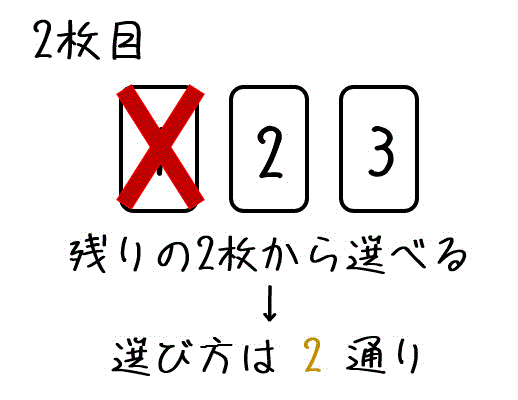
3




場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




順列と組み合わせの公式とその違い 問題付き 理系ラボ




数学a 場合の数 順列の問題か 組み合わせの問題かの見分け方 坪田塾 公式youtubeチャンネル Youtube



同じものを含む順列の問題 京極一樹の数学塾



3




同じものを含む順列と組合せは 同じ です 問題4選もあわせて解説 遊ぶ数学
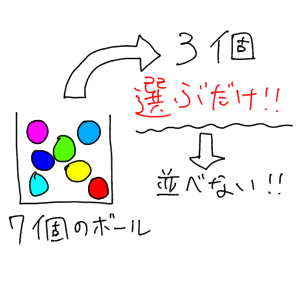



組み合わせ 並べない順列のこと 考え方と計算方法を解説 理数白書



Vuh56ueedqxkim




順列と組み合わせの公式とその違い 問題付き 理系ラボ




場合の数19 円順列と数珠順列 怜悧玲瓏 高校数学を天空から俯瞰する



2



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b




Pythonで階乗 順列 組み合わせを計算 生成 Note Nkmk Me
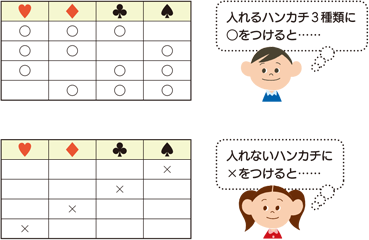



順列と組み合わせ 算数用語集
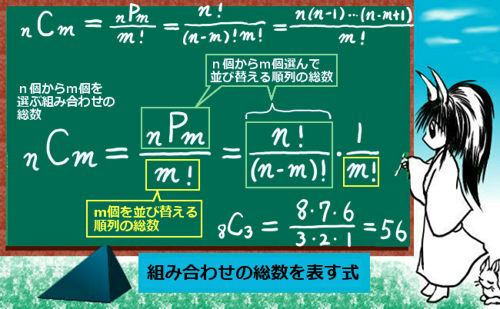



組み合わせの総数 場合の数 理数系無料オンライン学習 Kori
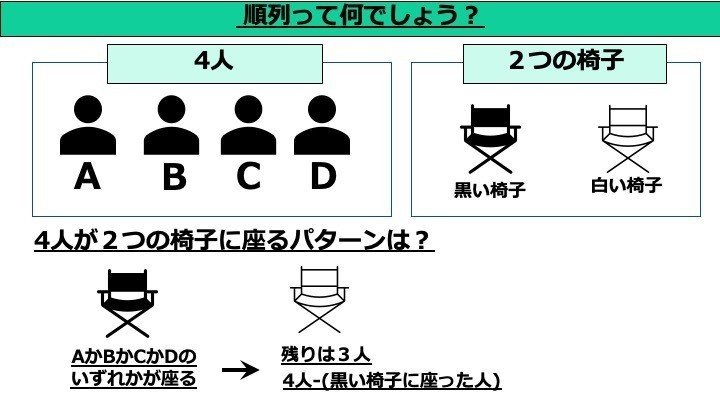



機械学習の統計学 順列と組み合わせって何 ししまる みらいのクルマをつくる人 Note



お気楽 Scheme プログラミング入門




Android 用の 順列 組み合わせ Apk をダウンロード




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ
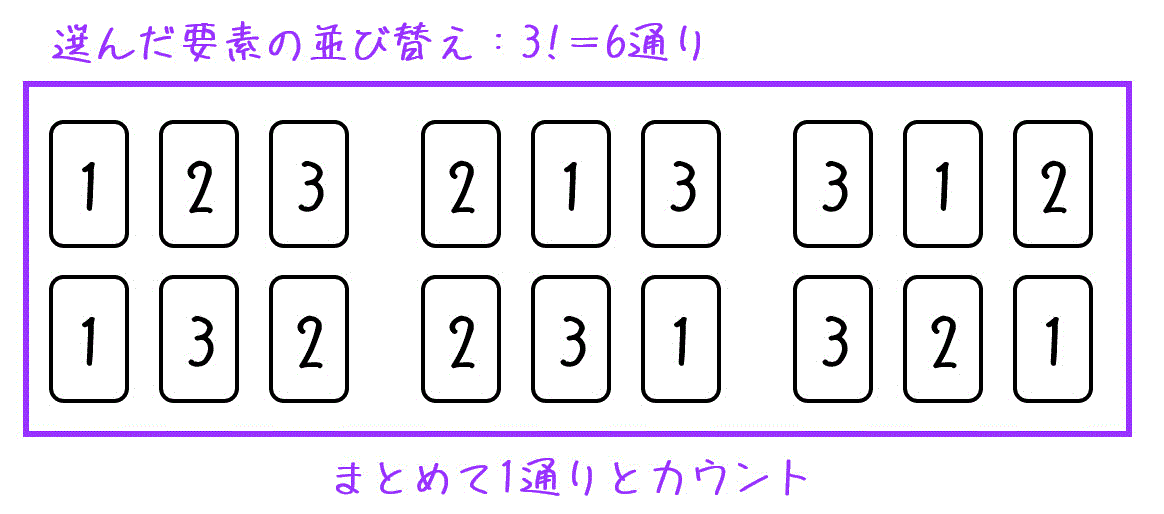



うさぎでもわかる場合の数 順列と組み合わせの違い 工業大学生ももやまのうさぎ塾



順列 組合せ記号 Pukiwiki



1




順列と組み合わせ Alis



順列と組み合わせの違いを基礎からわかりやすく解説 Youtube




順列pと組み合わせcの違いと 簡単 な見分け方




数学 P と C の 違い 確率の問題で コンビネーション C とパーミテーション P の違いを教えてください Amp Petmd Com




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




重複組み合わせ 重複順列って何してるの 場合の数 確率の頻出問題 良問 22 100 Youtube




順列と組み合わせの公式とその違い 問題付き 理系ラボ



順列と組み合わせの違いをリレーのチーム選考に例える コード7区




動画で解説 数学講座 順列と組み合わせのちがい ふじい塾 English Mathematics



順列と組み合わせの違い カンタンな見分け方を教えます Studyplus スタディプラス



順列と組み合わせ 算数用語集



同じものを含む順列の問題 京極一樹の数学塾




数列 順列 組み合わせ計算機 By Yoshiaki Onishi




重複順列と重複を許して取る組み合わせの違い がよく分かりません お願いします Clear




二項定理 二項定理のための 順列 組合せ 大人が学び直す数学



数学 P と C の 違い 確率の問題で コンビネーション C とパーミテーション P の違いを教えてください Amp Petmd Com



Spi M54e217p7lcis9d Com Jyunretu Kumiawase Q2



3分で分かる 順列と組み合わせの違いと公式をわかりやすく 練習問題つき 合格サプリ




重複を許す組み合わせ Hを使った公式 仕切りを使った考え方を解説 数スタ




高1 数a 場合の数 4 組合せ 高校生 数学のノート Clear




順列と組み合わせの公式とその違い 問題付き 理系ラボ



順列と組み合わせの違い カンタンな見分け方を教えます Studyplus スタディプラス




3分で分かる 順列と組み合わせの違いと公式をわかりやすく 練習問題つき 合格サプリ




うさぎでもわかる場合の数 順列と組み合わせの違い 工業大学生ももやまのうさぎ塾




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




Spi 数学 対策問題 組み合わせ 円順列 しかくのいろは




場合の数19 円順列と数珠順列 怜悧玲瓏 高校数学を天空から俯瞰する




順列と組み合わせの違いとは そしてそれぞれの意味を0から解説




1 順列と言える理由がわかりません ただサイコロ振っているものから判断するのなん Clear



3分で分かる 順列と組み合わせの違いと公式をわかりやすく 練習問題つき 合格サプリ




順列と組み合わせの公式とその違い 問題付き 理系ラボ



うさぎでもわかる場合の数 順列と組み合わせの違い 工業大学生ももやまのうさぎ塾




重複組合せはなぜ仕切りを使うの 整数解の個数を求める問題で鍛えよう 遊ぶ数学



重複組合せ
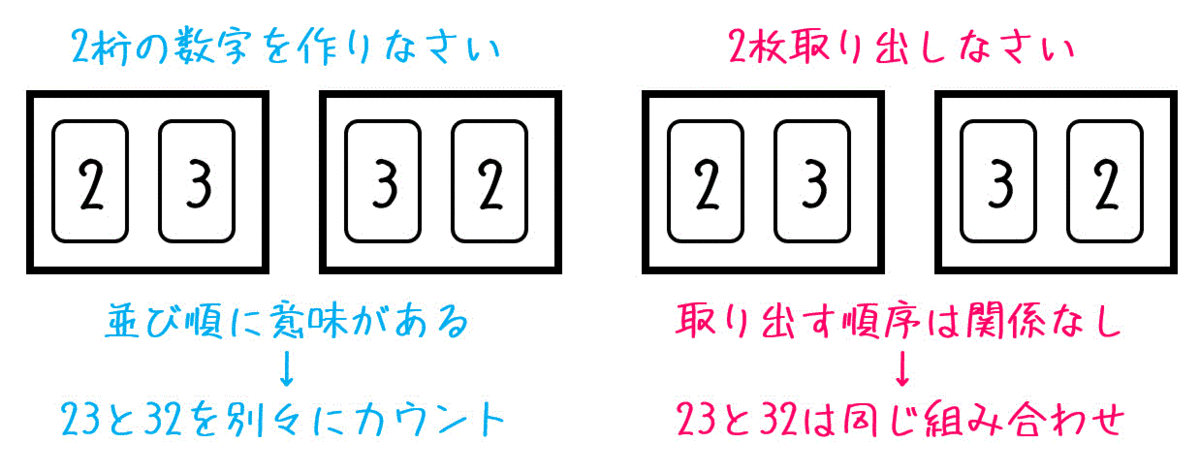



うさぎでもわかる場合の数 順列と組み合わせの違い 工業大学生ももやまのうさぎ塾
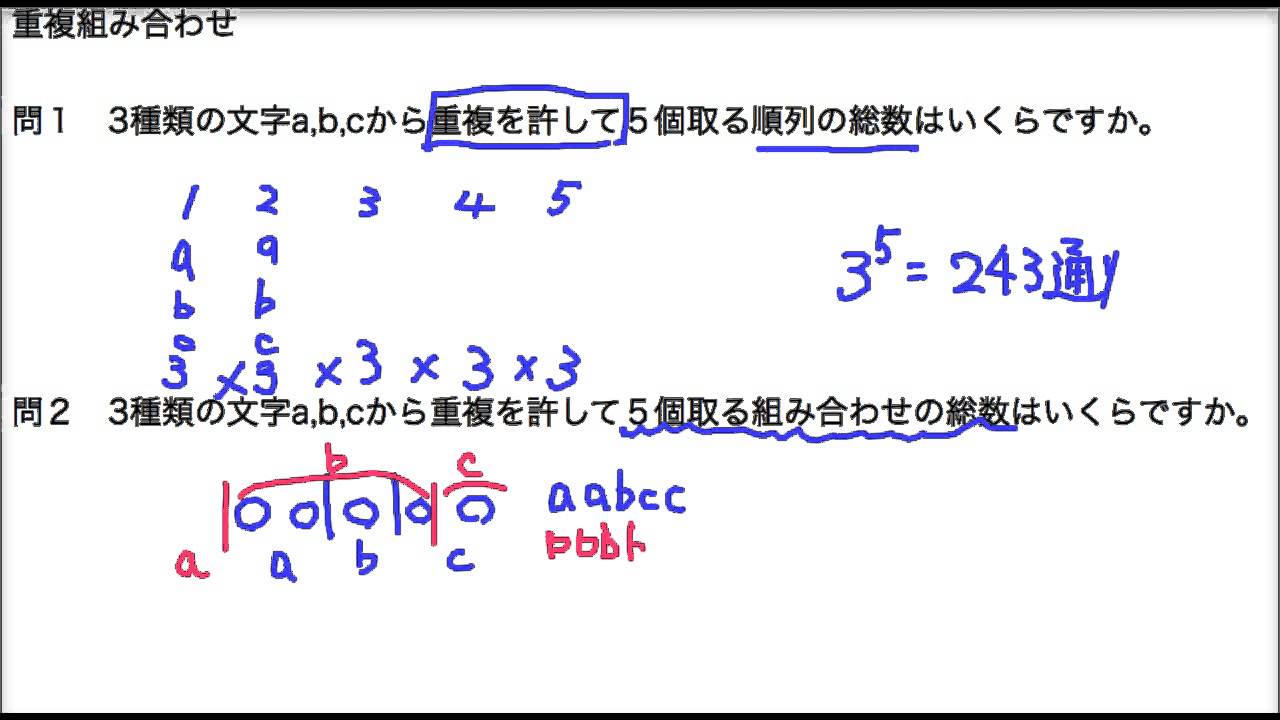



重複組み合わせ1 順列と組み合わせの違い Youtube
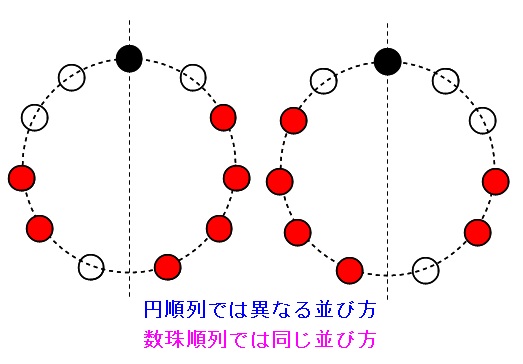



円順列と数珠順列の考え方や公式と問題の解き方



組み合わせ C とは 公式や計算方法 は何通り 受験辞典




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




順列と組み合わせの公式とその違い 問題付き 理系ラボ




Uたーん 勉強垢 V Twitter 順列と組み合わせについての質問を受けました 許可を頂いたのでその解説を公開します 参考にしてください ノートに書いて復習すると効果的なのでぜひ 気軽にdmで質問してください 数学 順列 組み合わせ 重複順列




順列と組合せの違いと例題 高校数学の美しい物語



組み合わせ C とは 公式や計算方法 は何通り 受験辞典




順列と組み合わせ 算数用語集




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学




順列と組み合わせの公式とその違い 問題付き 理系ラボ



順列と組み合わせを計算する Permut Combin関数 Excel関数




場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん



0 件のコメント:
コメントを投稿