で与えられる。これは点(a, b), (c, d)と原点とがつくる平行四辺形の面積である。 (つまり、この三角形の2まいぶん) 同様に、3次の行列 では、行列式 はそれぞれの点がつくる平行六面体の体積になる。 (これ対称行列になってるけど他意はない、 平行六面体の体積 行列式 外積は, ある一行が基底であるような行列式として書くことができた これを用いると, スカラー三重積は次のように計算できる なんと, 3つのベクトルが張る平行六面体の体積は成分を並べた3×3の行列式として計算できるのだ ここで, 2つのベクトルが張る平行四辺形平行四辺形の面積 (2辺と間の角度) ツイート 面積の計算 ・ 正三角形の面積 ・ 三角形の面積 (底辺と高さ) ・ 三角形の面積 (2辺と間の角度) ・ 三角形の面積 (1辺と両端の角度) ・ 三角形の面積 (3辺の長さ) ・ 正方形の面積

平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun
平行 四辺 形 体積
平行 四辺 形 体積- (6) 平行四辺形の面積・平行六面体の体積 外積を用いることで、ベクトルが張る平行四辺形の面積、ベクトルが張る平行六面体の体積を求めることができます。 (i) 平行四辺形の面積 2つのベクトル \( \vec{a} \), \( \vec{b} \) が張る平行四辺形の面積 \( S \) は\N次元超球の体積はヤコビアン、曲面積は平行四辺形 上野孝司 16年7月4日 N次元超球体積はヤコビアン、曲面積は平行四辺形 1.Γ関数と極座標変換―N次元球の体積はヤコビアン 1‐1.3次元と4次元球の体積 半径r の3次元球の体積 4 3




高校数学b ベクトルの外積 裏技 による法線ベクトル 空間の三角形の面積 平行六面体の体積 四面体の体積 受験の月
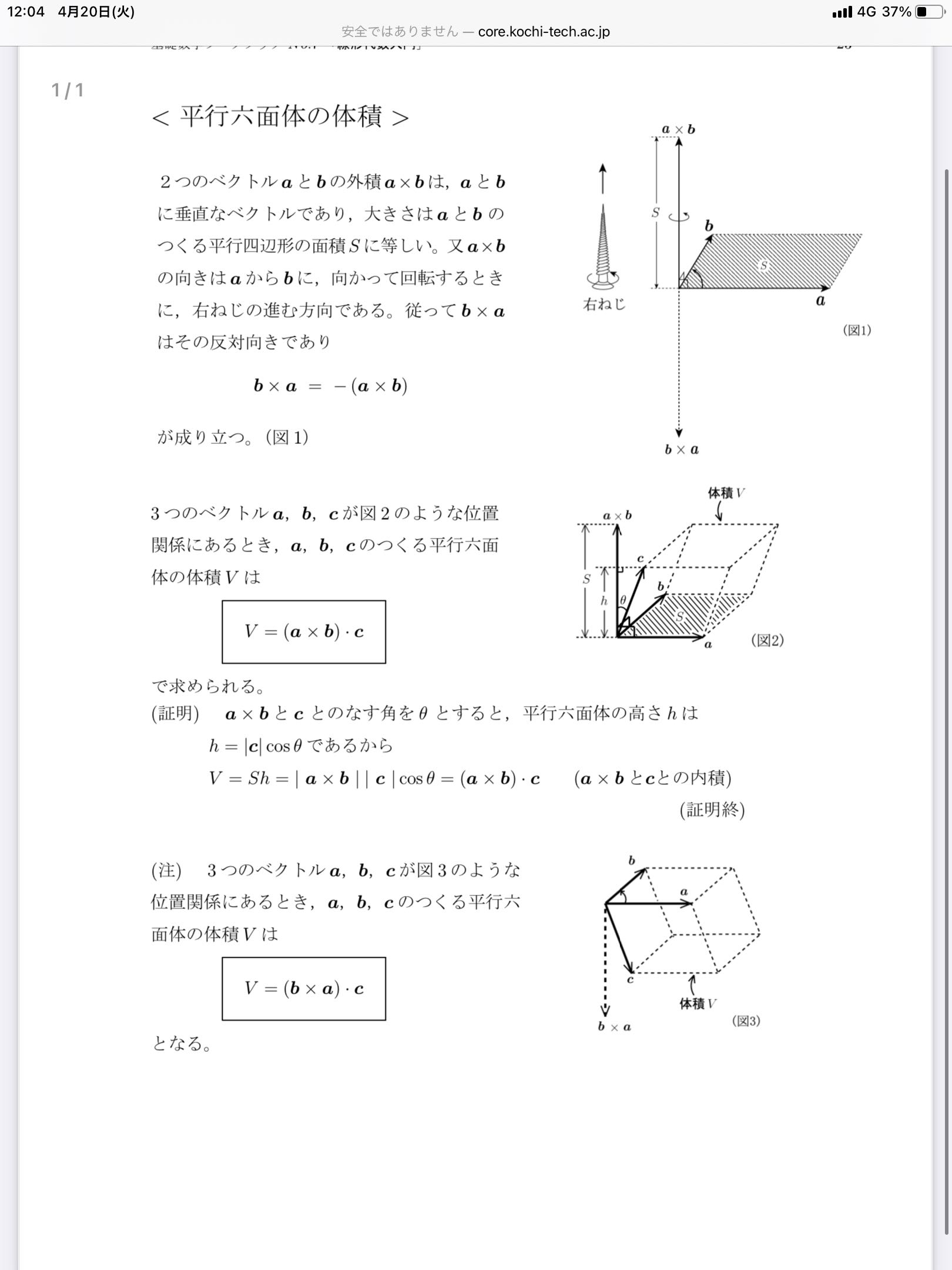
平行四辺形の面積=底辺×高さ (3)の正答例 底面積 説明 三角柱の体積は,角柱の体積の公式を使って求 めることができる。 底面の形が直角三角形なので,三角形の面積の 公式を使って底面積を求めると, 角柱の体積の公式は,底面積×高さなので,四角錐台の体積 110 /191件 表示件数 5 10 30 50 100 0 1 10 女 / 40歳代 / 会社員・公務員 / 非常に役に立った / 使用目的 建築設計の折り上げ天井の空調気積と平均天井高さ ご意見・ご感想 計算式も提示頂いてるので、根拠を示せるので助かり22 平行六面体の体積 空間ベクトル(3 次元ベクトル) a,b,c の作る平行六面体(下図) において, a ˆ b とc のなす角をθ とする a ˆ b はa,b の張る平面と直交するから, a,b の作る平行四辺形を底面と見たときの平行六面体の高さh は h " ∥c∥cosθ " ∥c∥¨ paˆbq¨c ∥aˆb∥∥c∥ paˆbq¨c
平行四辺形の面積 (底辺と高さ) ツイート 面積の計算 ・ 正三角形の面積 ・ 三角形の面積 (底辺と高さ) ・ 三角形の面積 (2辺と間の角度) ・ 三角形の面積 (1辺と両端の角度) ・ 三角形の面積 (3辺の長さ) ・ 正方形の面積7・平行四辺形の面積 5年 平行四辺形って? まず、平行四辺形と言うのはどういう四角形なのか、おさらい。 2組の対辺(向かい合った辺)が平行な四角形を平行四辺形と言います。参考:「その13図形の性質と集合・四角形」。 そして、覚えておいてほしい名前など。C2 とb2 の作る平行四辺形を立体の底面と見ると, b2 の終点をc2 の方向に動かしてもそ の平行四辺形の面積が変わらないので , 立体の体積も変わらない よって, a2 b2 c2 a2 b2 c2 c2 1 1 0 1 3 2 1 1 2 0 B @= a3 b3 c3 とおく
えば,長方形と平行四辺形について,平行四辺形 は長方形に変形できるという関係に着目し,平行 四辺形の面積を求める式を学習する。 本教材で扱う斜角柱の体積の求め方は,小学5 年生の平行四辺形の面積を求める学習を3次元に 拡張した内容である。平行四辺形の面積= 底辺 ×高さ 平行四辺形の面積=( 上底+下底 )×高さ 台形2つの面積=( 上底+下底 )×高さ 台形1つの面積=( 上底+下底 )×高さ÷2 とまあ、こんなわけで、台形の面積の公式が出来たわけですね。 後で説明しますが、三角形のここで,平行六面体の定義を示す34。 <定義> 角柱とは,数個の平面によってかこまれ,そ のうち二つの相対する平面が合同でかつ平行 であり,残りの平面が平行四辺形である立体 である。底面が平行四辺形となる四角柱を平 行六面体という。
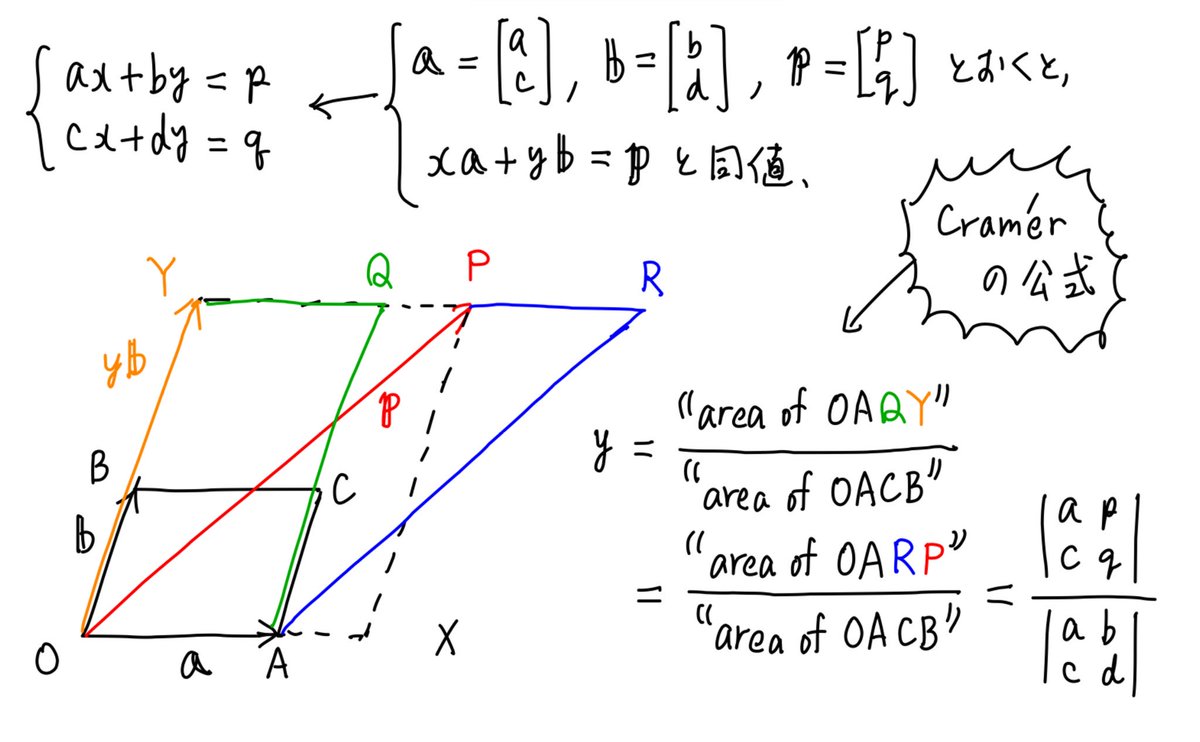



黒木玄 Gen Kuroki 数楽 添付画像は 2次元の場合のクラメールの公式が 行列式が 面積 符号が 向き を表す であることから 見た目的に 明らか な公式に過ぎないことの説明 平行四辺形の変形が 向き を変えないことも明らか N次元も同様



Http Www Soumu Go Jp Programming Data 017 017 01 02 Pdf
なので, 一般に, 右図のような平行四辺形になります(但し, b がa の定数倍であるとき, ∆ A) は平行四辺形でなく, 線 分になります) x1 x2 a = (a1;a2) b = (b1;b2) a b ここで, 次の3つに場合分けして考えていきましょう: (1) a1b2 a2b1 = 0 (2) a1b2 a2b1 ̸= 0, a1 ̸= 0 (3) a1b2 a2b1底面が平行四辺形の四角 柱や底面が三角形の三角柱 の体積も「底面積×高さ」 で求められるかを調べる活 動を通して,角柱の体積も 「底面積×高さ」で求めら れることを理解することが できる。 1 問題をつかみ,課題を設定する。(三角形の面積) 折り紙でかざりを作ろう①(平行四辺形や三角形の面積) 折り紙でかざりを作ろう②(平行四辺形や三角形の面積) 平行四辺形の面積は?(いろいろな四角形) 直方体をならべて立方体を作ってみよう(直方体・立方体の体積、公倍数)



Math 回転体の体積 表面積とパップス ギュルダンの定理 働きアリ



回るとどうなる 回転体の 体積 名寄 算数数学教室より
長方形の面積 平行四辺形の面積 三角形の面積 台形の面積 円の面積 算数では様々な公式を覚えます。 しかしその公式の意味を知っている方は多くないと思います。 本ホームページでは公式の意味や公式の導き方を図を使用して分かりやすく説明して(1)左の図の木の葉はおよそどんな形で あるといえますか。 答え 平行四辺形 (2)この木の葉のおよその面積を求めま しょう。 およそ答え 宮城スタジアム (4) 3=12 12cm2 平行四辺形の面積を求める公式は, 「底辺×高さ」です。三角形,四角形の合同 円周,円周率 三角形,四角形,平行四辺形, 台形,ひし形の面積 直方体,立方体 見取図,展開図 面積の単位 (cm 2,m,km,a,ha) 長方形,正方形の面積 ものの位置の表し方 角柱,円柱 角柱・円柱の体積 箱の形




ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun




高校数学b 平行六面体と空間ベクトルの演算 受験の月
小学4年生の算数・台形・平行四辺形・ひし形・対角線の問題を繰り返し練習できるプリントです。 小学5年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 平行六面体の体積は次の式で求められます。 V = S * h、ここでhはこの平行六面体の高さ、Sはその底辺の面積であり、その位置は上記で考察した。 上記で解決された問題を含む例を検討することができます。 平行四辺形の底面の面積は150cm²、高さは40 cmによって作られる平行四辺形がxy 平面に含まれるという条件である.よって,この平行四辺形を平行 六面体の底面と見るとその高さはa3 のz 座標の絶対値となるので,P(a1;a2;a3) の体積が底面積 高さで与えられることから,この等式が成立する.)



1



図形の回転 第2問 ラ サール中学 入試算数問題 類題 浅野中学 03年 入試算数問題 類題 まいにち一題 中学受験過去問題研究
三角形は2つ合わせると 平行四辺形になります。 平行四辺形の半分だから 下底 上底と同じ 高さ 底辺 上底 高さ 台形も2つ合わせると 平行四辺形になります。 ひっくり返して横に並べ ると、もとの台形の2倍の 平行四辺形になります。線形独立 空間ベクトル→−a , b, →c は,始点を同じにしたとき,同一平面上に ないならば線形独立,同一平面上にあるならば線形従属であるとい う。(第1 章§2 参照) それは,行列式で次のように判定できる。命題 ⃗a = t(a 1,a2,a3),⃗b = t(b1,b2,b3),⃗c = t(c1,c2,c3) が線形独立平行六面体の符号付き体積についても, 平行四辺形の符号付き面積と同様の議論により , 𝑉 ± 𝑎 1




ベクトル三重積と平行六面体及び四面体の体積 身勝手な主張



1
日本大百科全書(ニッポニカ) 平行六面体の用語解説 二つずつ平行な三組の平行平面で囲まれた立体を平行六面体という。平行六面体の六つの面はすべて平行四辺形である。同一の面上にない頂点を結んでできる四つの線分を対角線という。対角線は1点で交わり、その交点が各対角線の中点に平行四辺形とは、2組の平行で合同な側面を持つ4辺の図形を指します。 たとえば、正方形は平行四辺形です。 ただし、平行四辺形は4つの90度の角度を持つ必要がないため、すべての平行四辺形が正方形であるわけではありません。 平行四辺形は2次元の形状なので、面積を見つけることができは、もとの平行四辺形ではどこの長さになるか を考え、底辺と高さについて理解する。 2 底辺と高さという言葉を使って平行四辺形の 面積の公式をつくる。 技 平行四辺形の面積を求める適用問題をする。 1 等積変形などを利用して、面積の求め方を




平行四辺形の対角線の長さの求め方




Abcd 2 A Lihat Cara Penyelesaian Di Qanda
形でまとめることについても理解させる。 本単元では,第4 学年,第5 学年で学習した長方形,正方形,三角形,平行四辺形の面積や立体の 体積や第6 学年で学習した円の面積の学習で学んだことを生かし,一般化して角柱や円柱の体積を求行列式 線型代数 数学教育 二つのベクトル v 1, v 1 が張る平行四辺形の面積を考える: v 1, v 1 を数ベクトルに表す: 平行四辺形の面積は,つぎの計算で求められる: (a 11 + a 21 ) × (a 12 + a 22 ) ー( a 11 × a 12 + a 21 × a 22 + 2 × (a 12 × a 21) ) = a 11 × a 結論を述べると,2次正方行列の行列式は平行四辺形の面積である. 下図を見て欲しい.行列 A の1列目が橙色ベクトル,2列目が緑色ベクトルで,それらを2辺とする平行四辺形の面積が行列式 A だ.これは簡単に示すことができる.平行四辺形を含む長方形の面積から,平行四辺形の外



算数道場 4 面積と体積 1 面積の意味と単位 その7 平行四辺形の面積




平行四辺形の面積の求め方 公式と計算例




高校数学b ベクトルの外積 裏技 による法線ベクトル 空間の三角形の面積 平行六面体の体積 四面体の体積 受験の月




平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun




ベクトルの外積と平行四辺形の面積 身勝手な主張



平行四辺形の面積の公式 算数の公式




数学質問 平行四辺形を回転させてできる立体 Youtube
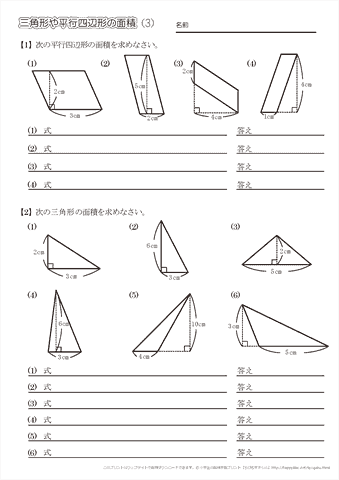



小学5年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生



Left 2right 1 1 2 Aleft Descubre Como Resolverlo En Qanda




ベクトルの外積と平行四辺形の面積 身勝手な主張




モデルの体積を計算する 試行錯誤
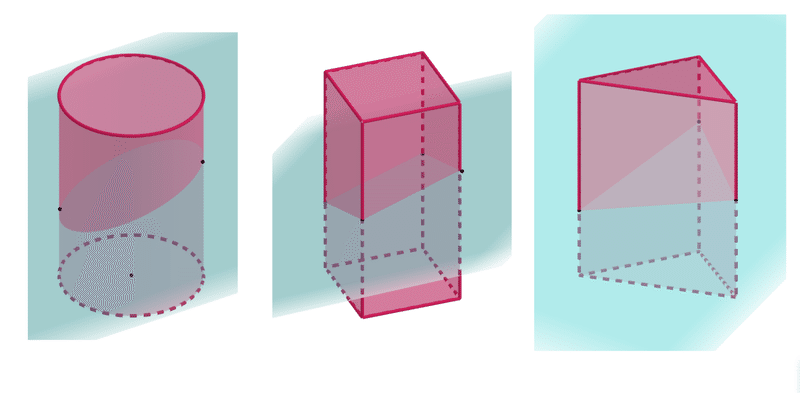



立方体の切断 断頭柱体のうち 底面が円 平行四辺形 三角形のものの体積は 底面積 高さの平均 ワンセンテンス算数 Note
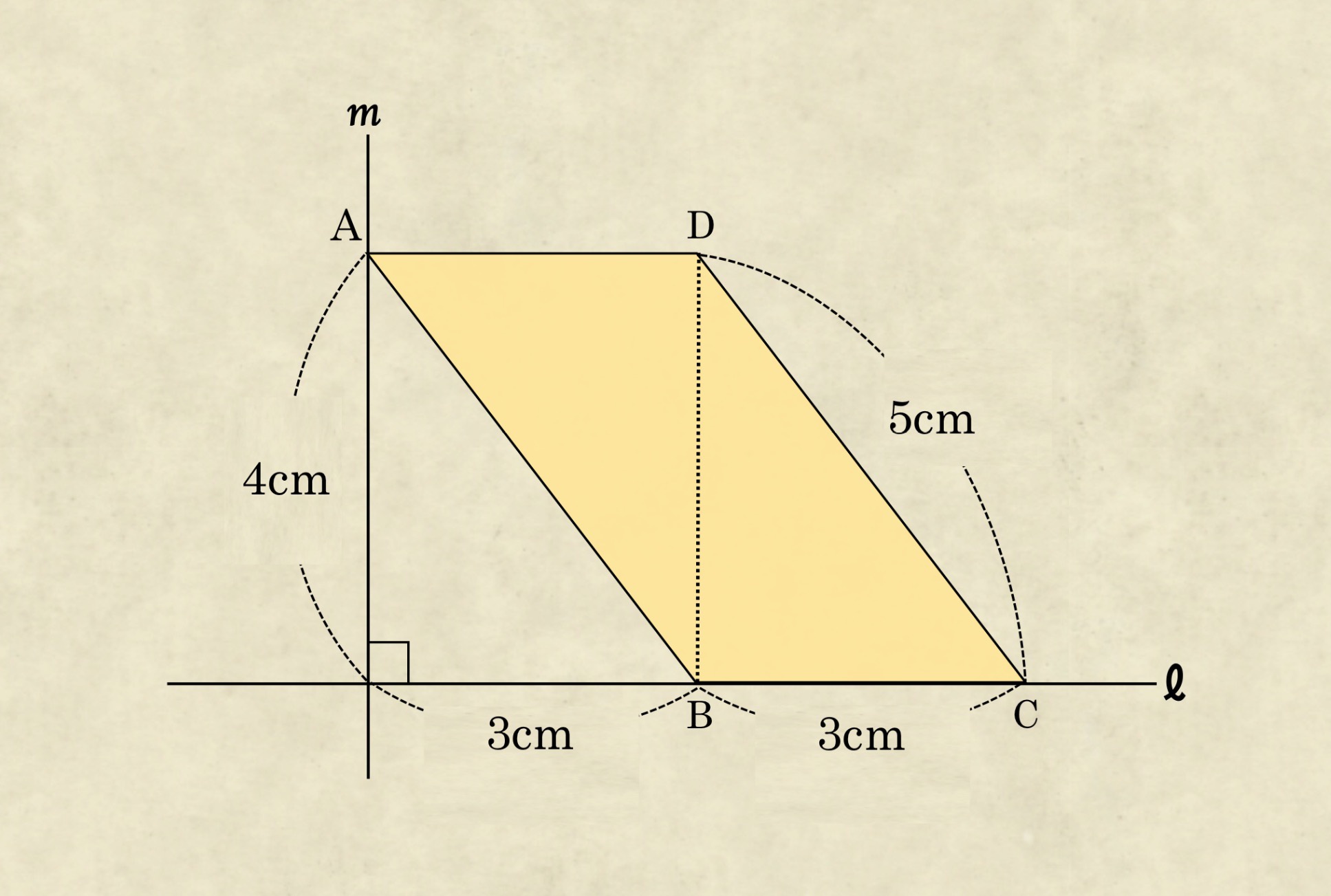



17年2月号の巻 難攻不落の算数城攻略 忍者エピス丸 Epis Education Centre Epis Education Centre



第81問の解答



柱体の切断上の立体は 底面が平行四辺形で 隣の式のように体積が求まります Yahoo 知恵袋




高校数学 平行四辺形の面積の求め方 練習編 映像授業のtry It トライイット




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ



回転体 中学受験ー算数解き方ポータル




小5 算数 小5 41 平行四辺形の面積 Youtube




平行四辺形の定理や定義 平行四辺形の覚えておきたい性質は4つ 中学や高校の数学の計算問題




Left 2right 1 1 2 Aleft Descubre Como Resolverlo En Qanda
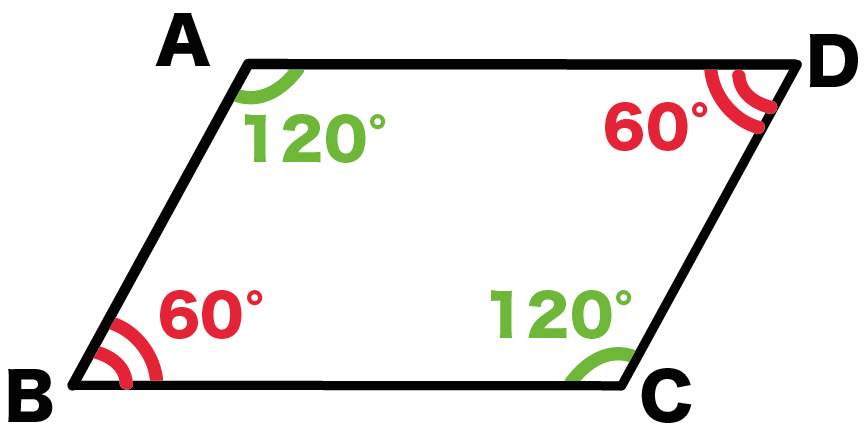



中2数学 平行四辺形の3つの性質 Qikeru 学びを楽しくわかりやすく




平面図形の面積 まとめ1 2 平行四辺形の面積の求め方 Youtube
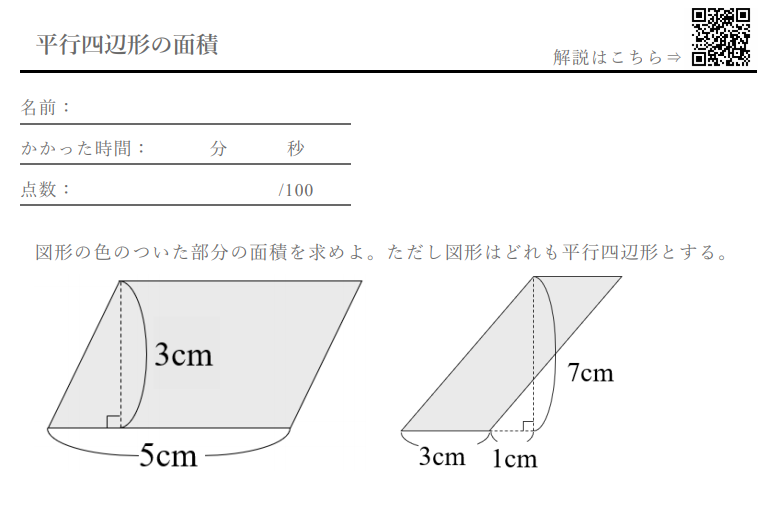



平行四辺形 の面積 計算ドリル 問題集 数学fun




高校数学 平行四辺形の面積の求め方 例題編 映像授業のtry It トライイット
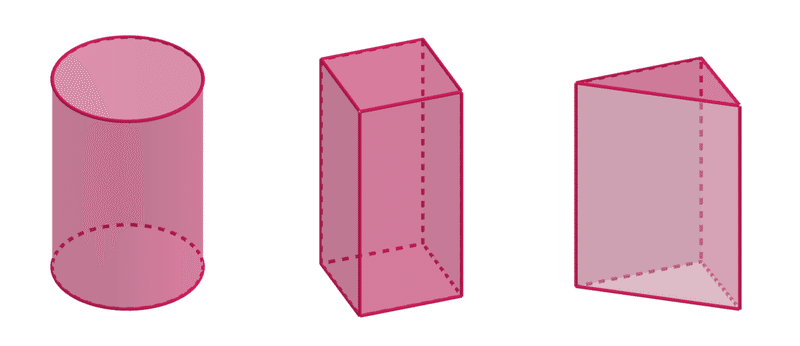



立方体の切断 断頭柱体のうち 底面が円 平行四辺形 三角形のものの体積は 底面積 高さの平均 ワンセンテンス算数 Note
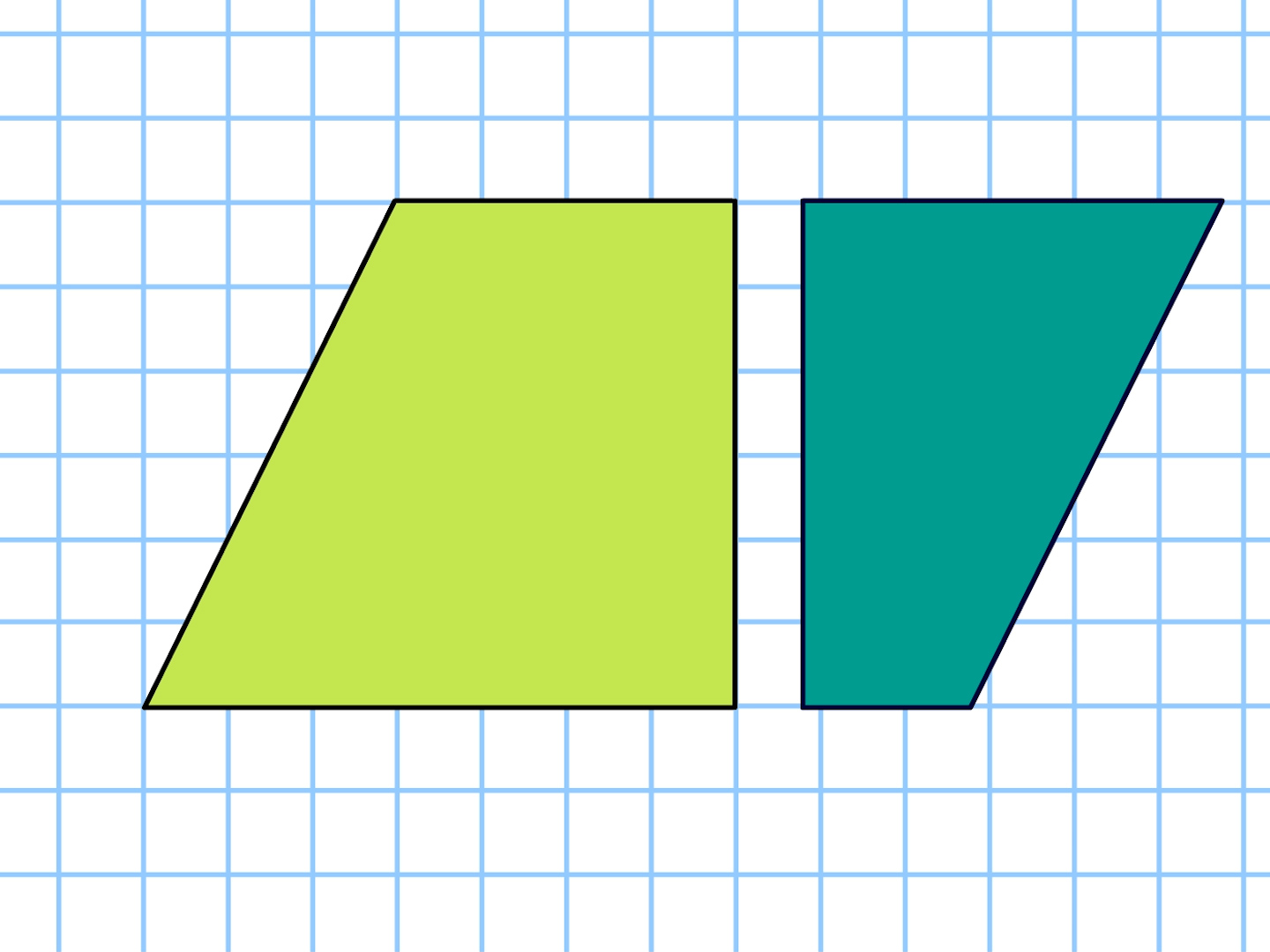



5年 平行四辺形の面積 算数イメージ動画集 大日本図書




平行四辺形の面積の求め方 公式と計算例
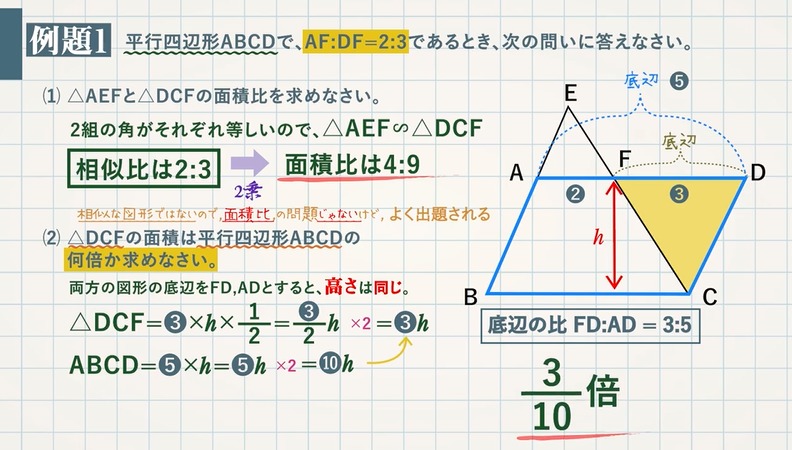



面積比と体積比 教遊者



1



1
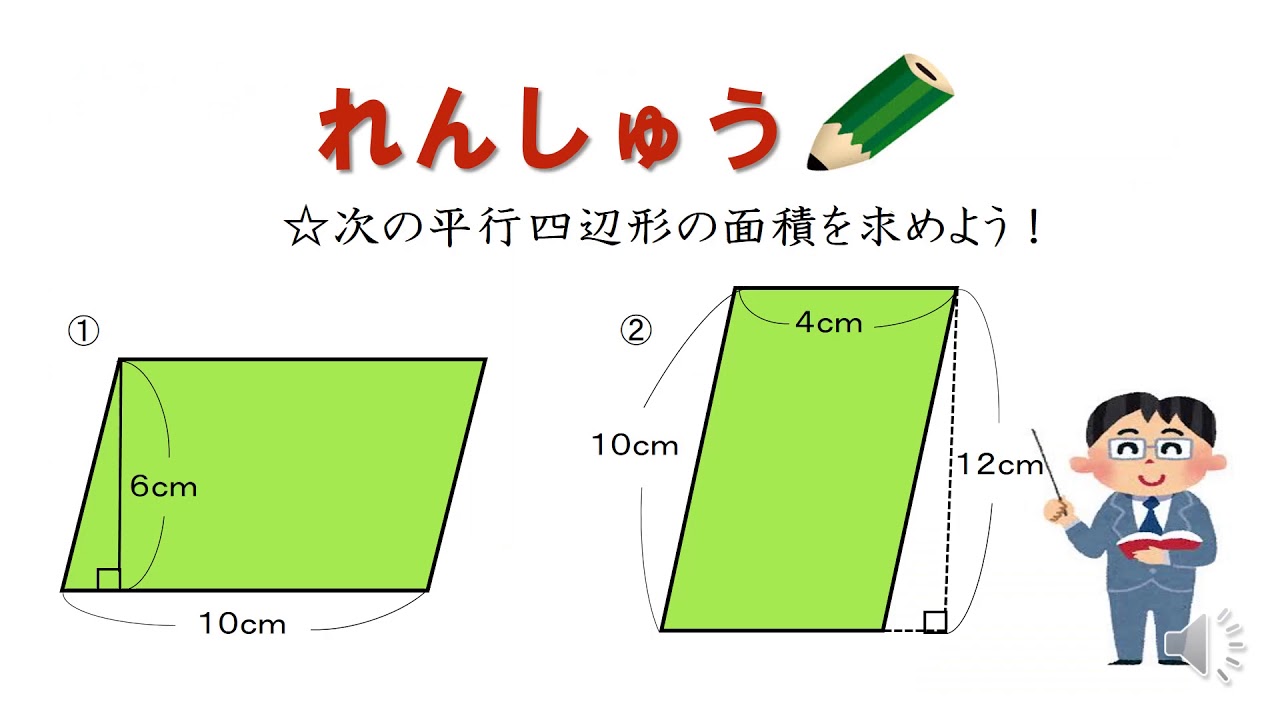



小5 面積の求め方を考えよう 平行四辺形 日本語版 Youtube
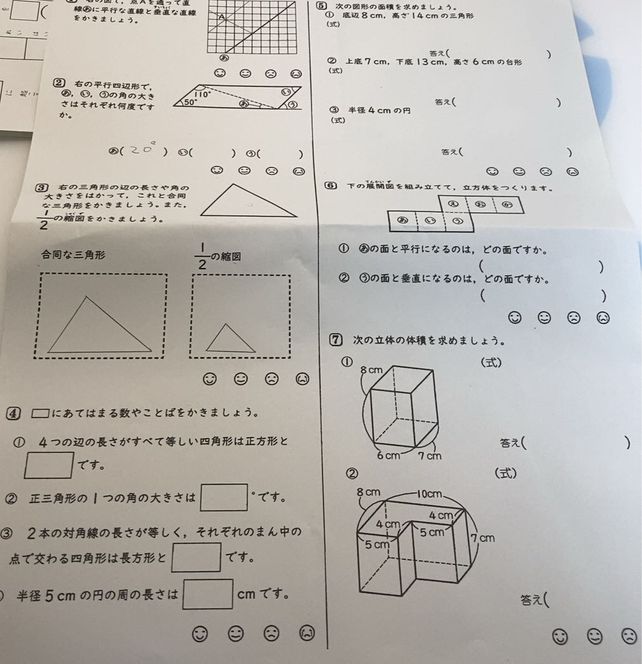



Bar2 110 O 50 A 8 Left 2 Descubre Como Resolverlo En Qanda
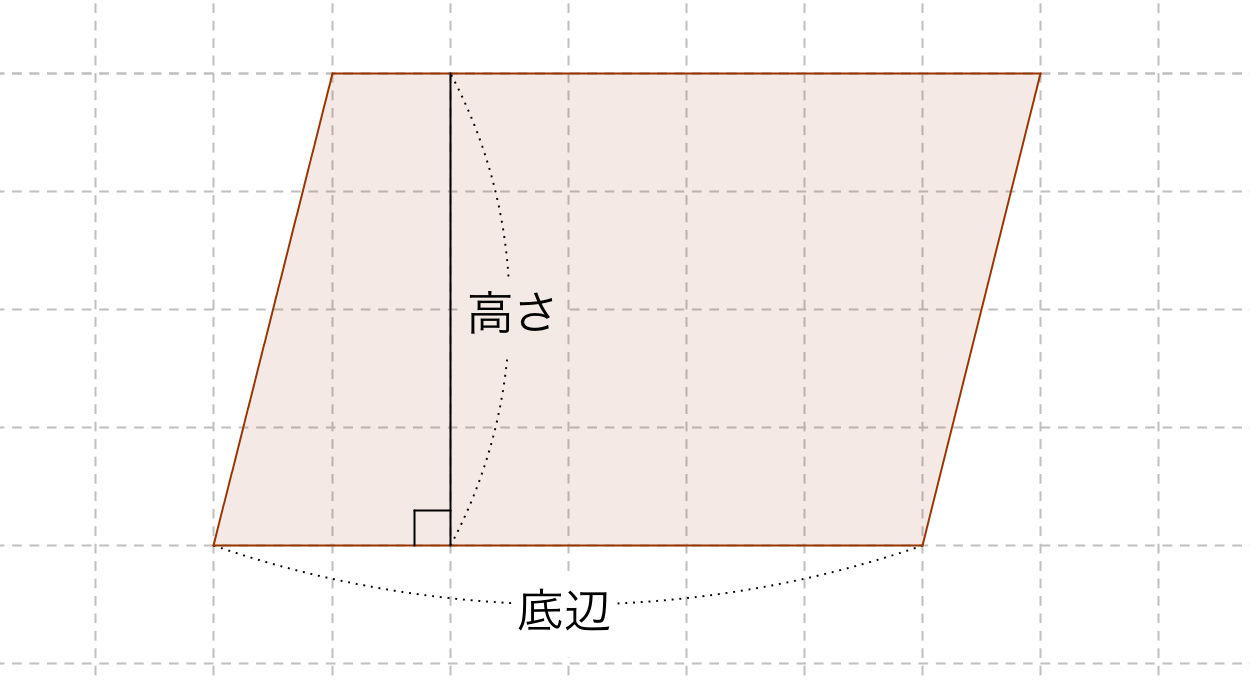



平行四辺形の面積の公式 算数の公式



算数道場 4 面積と体積 1 面積の意味と単位 その7 平行四辺形の面積
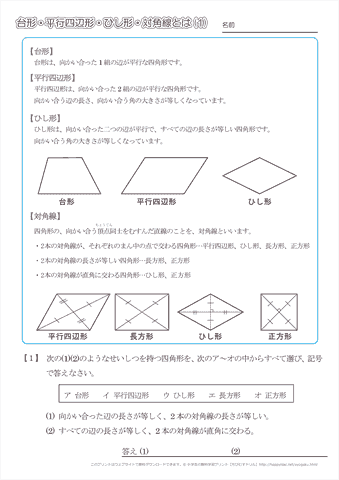



小学4年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生



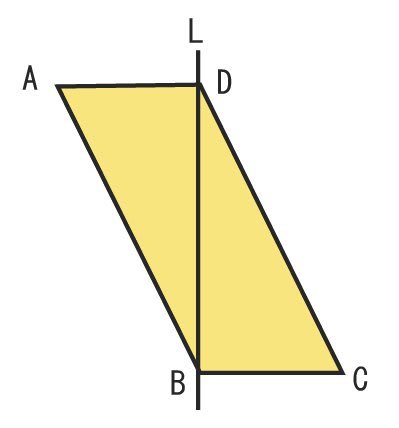
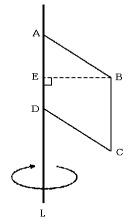
教えてください 図のような平行四辺形abcdを直線lを軸として1回転させ Yahoo 知恵袋
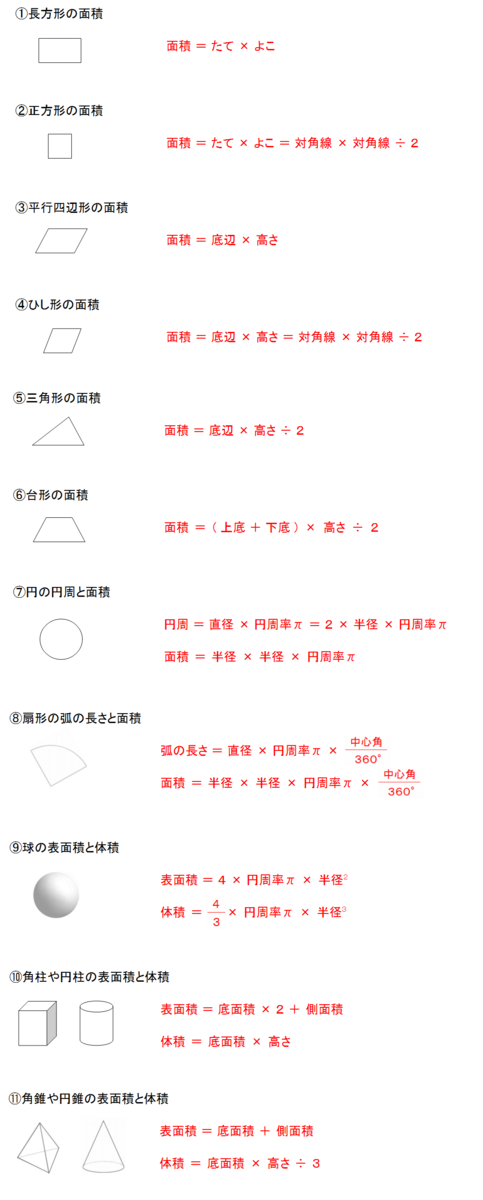



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師




ベクトル編 ベクトルで色々な図形を表現する 大学1年生もバッチリ分かる線形代数入門




平行四辺形の面積の求め方 公式と計算例



平行四辺形が回転すると 高槻中学 12年 中学受験ー算数解き方ポータル




モデルの体積を計算する 試行錯誤



2




簡単公式 ひし形 菱形 の面積を計算できる2つの求め方 Qikeru 学びを楽しくわかりやすく




平行四辺形の面積 ベクトルでの公式 理数系無料オンライン学習 Kori




塾 学校 家庭を結ぶ 受験情報サイト 学びネット




平行四辺形の面積の求め方 公式と計算例
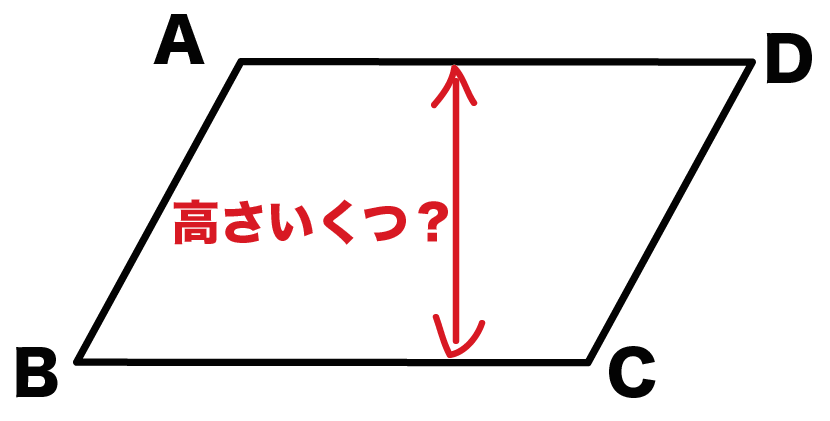



中学数学 平行四辺形の高さの2つの求め方 Qikeru 学びを楽しくわかりやすく




勉強しよう数学3c エディントンのイプシロンと行列式とベクトルの外積




平行四辺形の面積の求め方 公式と計算例
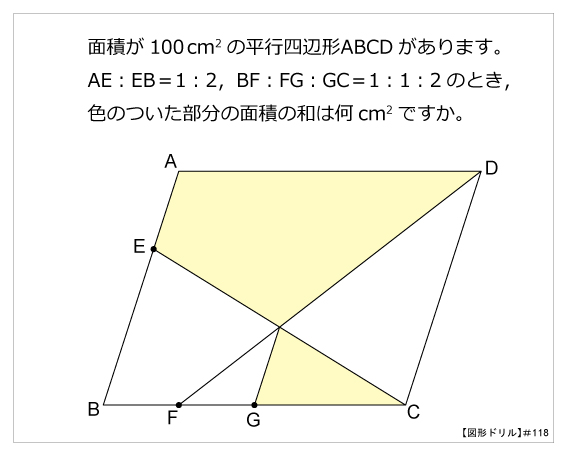



図形ドリル 第118問 平行四辺形の面積の和 算数星人のweb問題集 中学受験算数の問題に挑戦
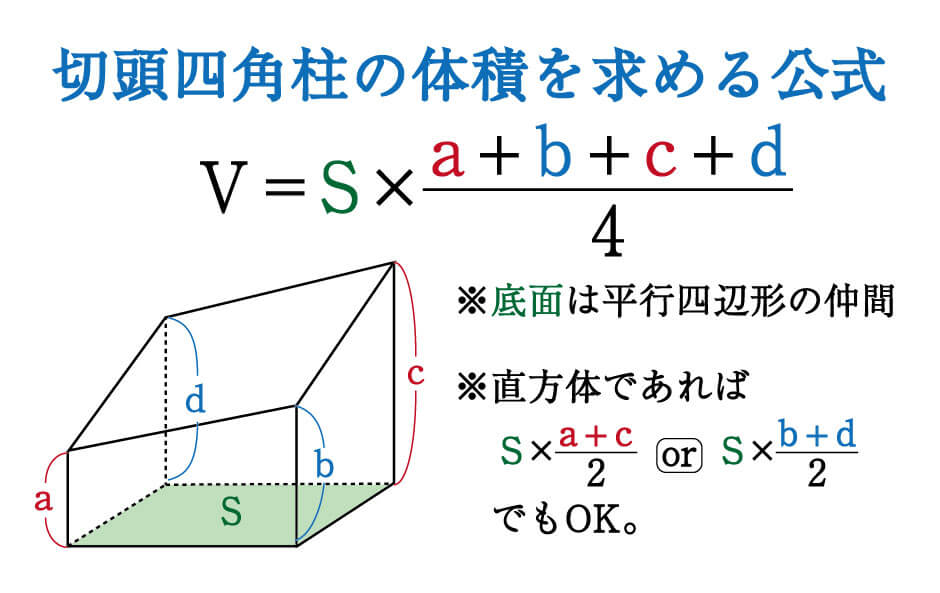



数学 斜めに切断された円柱 四角柱の体積は こう解くべし 受験の秒殺テク 6 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




相似 平行四辺形と面積比の問題を徹底解説 数スタ



回転体 中学受験ー算数解き方ポータル
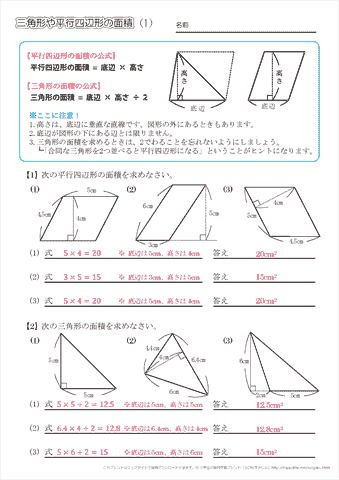



小学5年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生
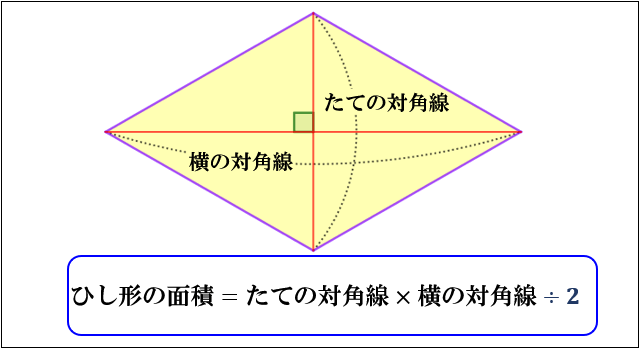



四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ
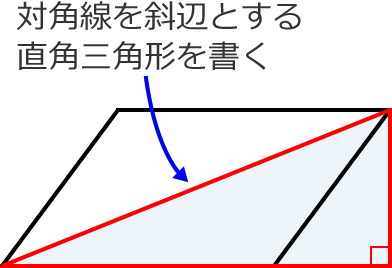



平行四辺形の対角線の長さの求め方



平行四辺形の問題で体積 の出し方が分かりません Tattann1511 Yahoo 知恵袋




大学入試過去問 検索結果
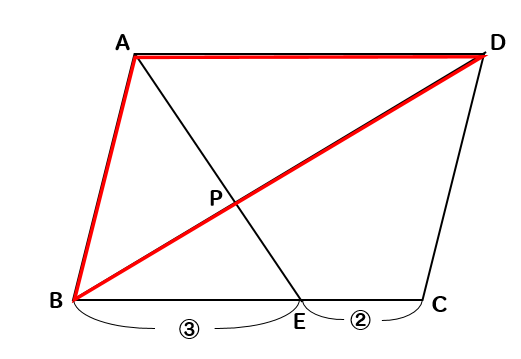



相似 平行四辺形と面積比の問題を徹底解説 数スタ




平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun



第5章21 面積の比と体積の比 平方四辺形の相似比と面積比 フロントエンドなブログ
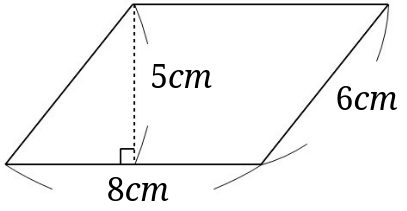



平行四辺形の面積の求め方で習う公式は なぜ底辺 高さになるの みけねこ小学校




Math 回転体の体積 表面積とパップス ギュルダンの定理 働きアリ
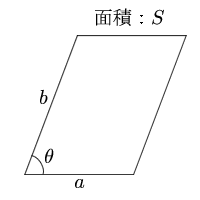



平行四辺形 2辺と間の角度 面積の計算 計算サイト




平行四辺形の対角線は中点で交わる ことの説明 おかわりドリル
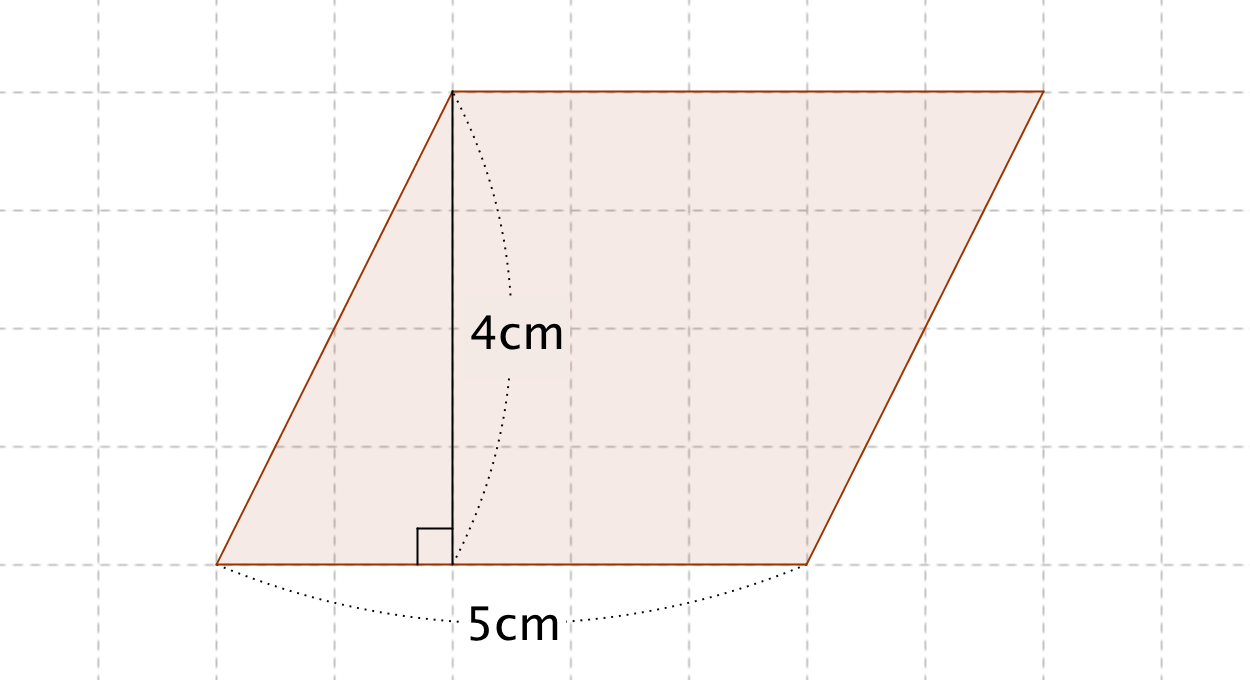



平行四辺形の面積の公式 算数の公式




高校数学 平行四辺形の面積の求め方 例題編 映像授業のtry It トライイット




底面が平行四辺形の四角柱の体積について考えました 6年算数 茎崎学園 つくば市立茎崎第二小学校




3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ
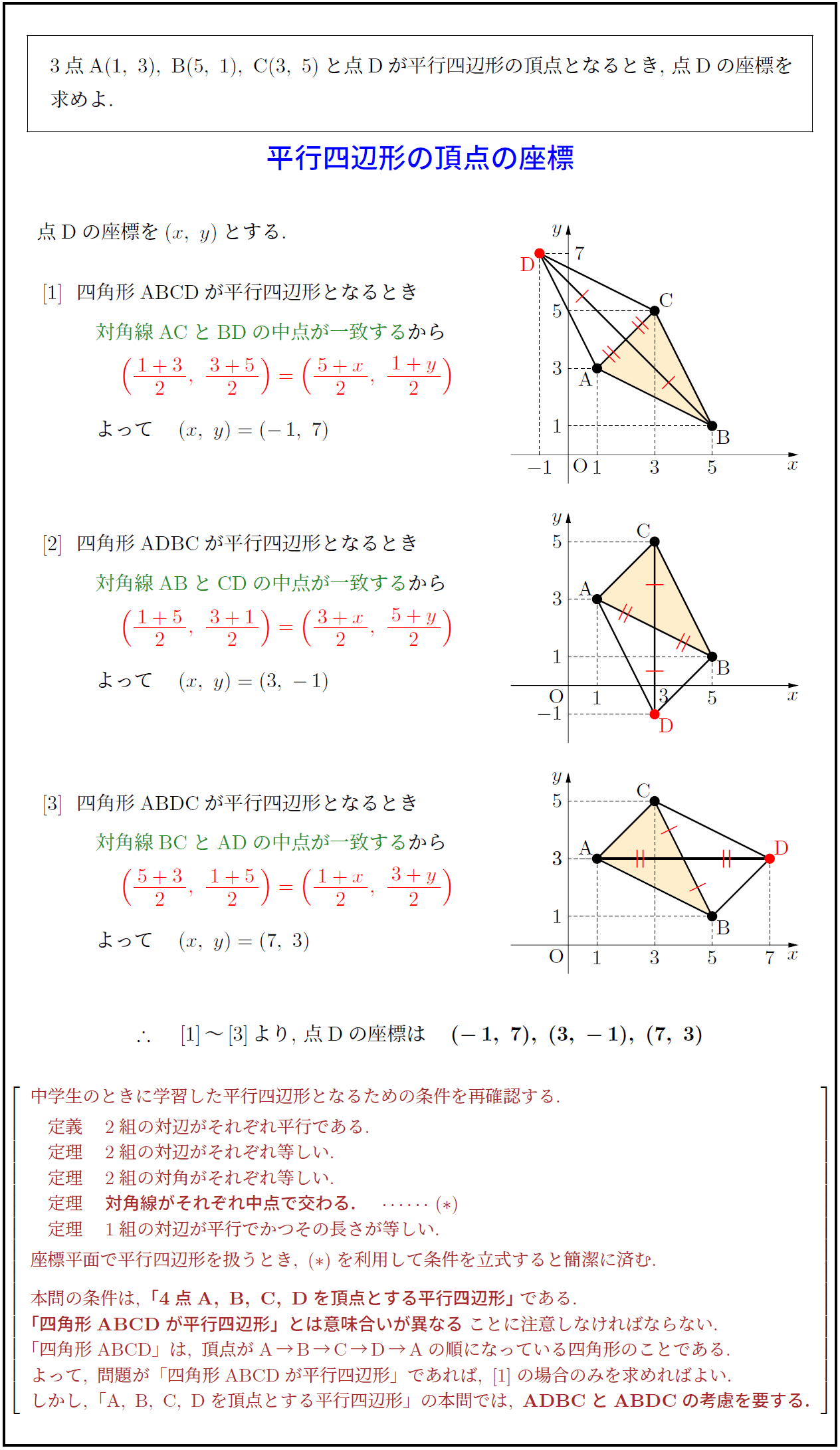



高校数学 平行四辺形の頂点の座標 受験の月
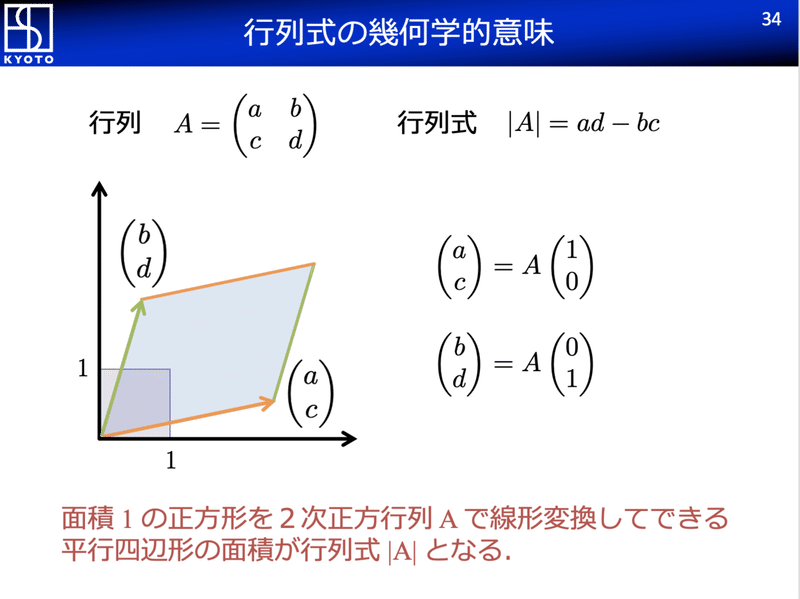



行列式 A Ad の幾何学的意味 Dr Kano Note




立方体の切断 断頭柱体のうち 底面が円 平行四辺形 三角形のものの体積は 底面積 高さの平均 ワンセンテンス算数 Note




平行四辺形の面積を求める公式 あまり知られていないかも 中学や高校の数学の計算問題




斜軸回転体の体積 応用編 傘型積分 おいしい数学




この2問の問題の解き方教えていただきたいです Clear



第81問の解答




簡単公式 平行四辺形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
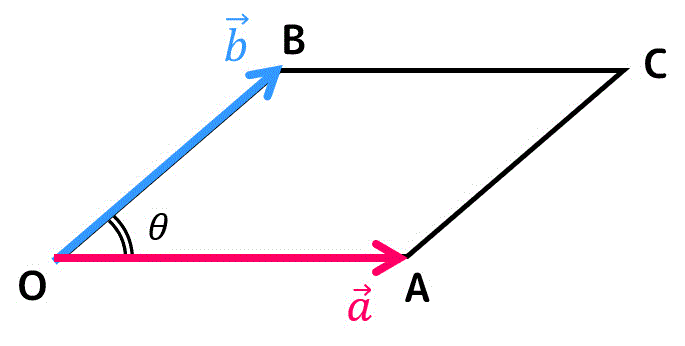



うさぎでもわかる線形代数 補充1 線形代数におけるベクトル 内積と外積 工業大学生ももやまのうさぎ塾



立体の体積は 2015年 大宮開成中学 どう解く 中学受験算数
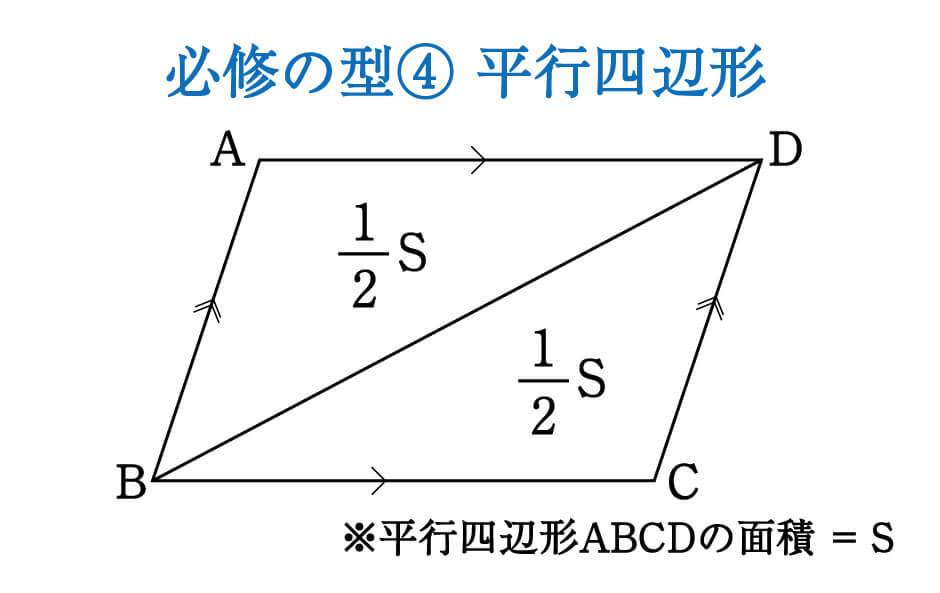



数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




平行四辺形の対角線の長さの求め方



大妻中野中学校入試問題のポイント



回転体 中学受験ー算数解き方ポータル




面積比 Youtube
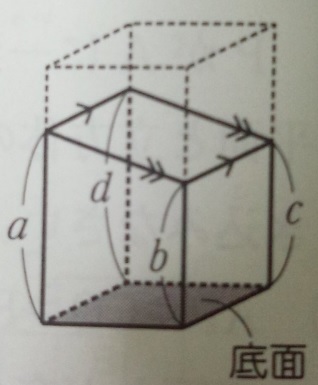



立体図形を斜めに切断した時の体積は 底面積 高さの平均 中学受験 塾なし の勉強法




平行四辺形で知っておくべきこと 苦手な数学を簡単に




5年 直方体と立方体の体積 算数イメージ動画集 大日本図書



立体の体積は平行線でね 基本に忠実に本質を伝える 楽天ブログ




5年生で 様々な図形の面積の求め方を習いますが ここでは 平行四辺形と三角形の面積の求め方を学習する自主学習ノートの例を紹介します 平行四辺形と三角形の面積を求める 三角形の面積 学習 学習ノート 子どもたちの研究




立方体や直方体の体積の求め方を習ったら 少し応用的な問題にも取り組みましょう 展開図を見て 体積を求める問題や いくつかの立方体や直方体の面積を足したり引いたりして解く問題です 学習ノート 小学校 算数 学習




この問題の答えにeprqは平行四辺形とかかれていて その理由がわかりません 教えて下 Clear



0 件のコメント:
コメントを投稿